Предмет: Алгебра,
автор: baronvpomosh9999
Помогите пожалуйста решить функцию, даю 45 баллов
Приложения:
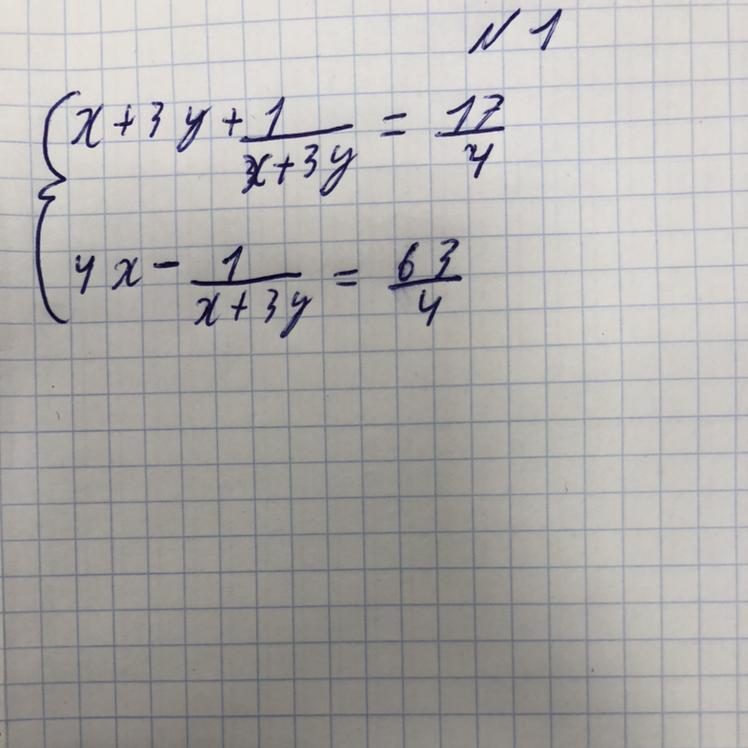
Ответы
Автор ответа:
1
Объяснение:
Рассмотрим первое уравнение:
Пусть х+3у=t ⇒
Ответ: (4;0) (79/16;-25/16).
Похожие вопросы
Предмет: Русский язык,
автор: alika84
Предмет: Русский язык,
автор: Ризван1
Предмет: Другие предметы,
автор: ликон3
Предмет: Українська мова,
автор: Valeria121705
Предмет: Математика,
автор: нана5553