Предмет: Математика,
автор: mr037860
Решить дифференцированое уравнение
Приложения:
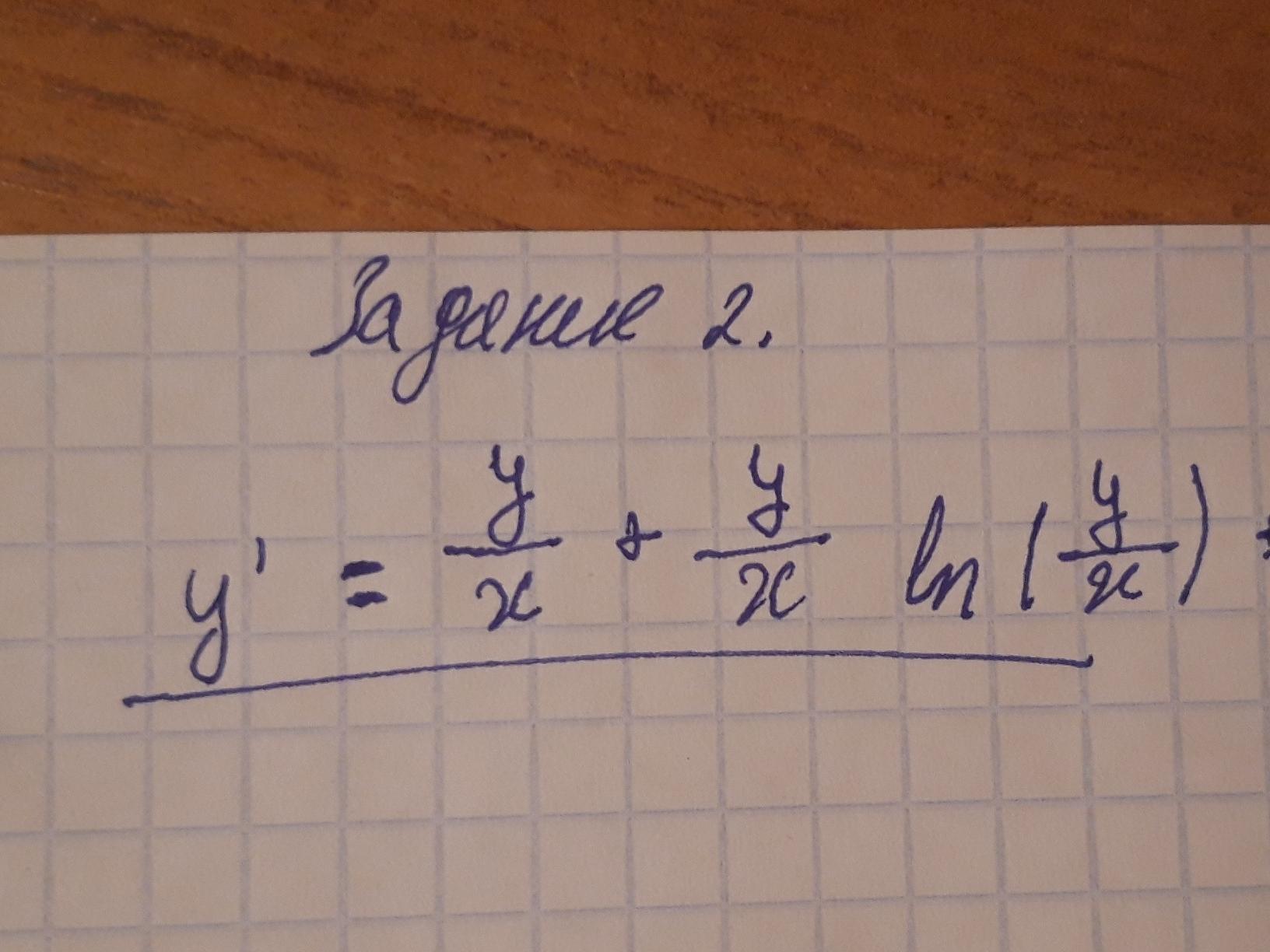
Ответы
Автор ответа:
0
Ответ:
Это однородное ДУ
Замена:
общее решение
mr037860:
спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: Ева2003111
Предмет: Русский язык,
автор: ashalaeva0703
Предмет: Русский язык,
автор: artembednyakov
Предмет: Қазақ тiлi,
автор: лучший50
Предмет: Математика,
автор: султан84