Question

4. Основанием треугольной пирамиды является равнобедренный тре- угольник с боковой стороной a и углом α при основании. Двугранные углы пирамиды при рёбрах основания равны β. Найдите:
1) площадь боковой поверхности пирамиды;
2) высоту пирамиды.

Answer 1

Ответ:

$\boxed{ S_{b} = \dfrac{a^{2} \cos \alpha \sin \alpha}{\cos \beta } }$

$\boxed{ OK = \dfrac{a \cos \alpha \sin \alpha \ tg \ \beta}{(1 + \cos \alpha)}}$

Объяснение:

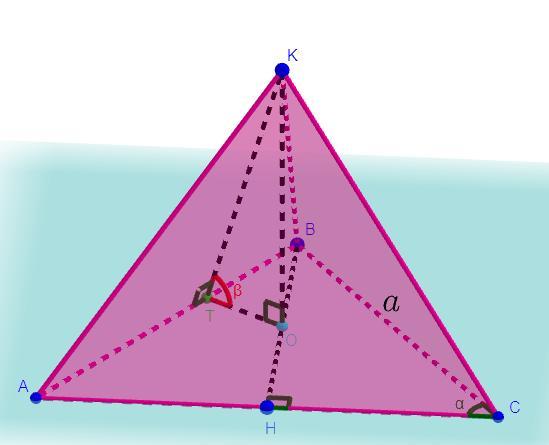
Дано: KABC - пирамида, BC = a, ∠ACB = α, ∠(KAC, ABC) = ∠(KBC,ABC) = =∠(KAB,ABC) = β, OK ⊥ ABC, AB = BC

Найти: $S_{b}, KO \ - \ ?$

Решение:

Рассмотрим равнобедренный треугольник ΔABC. Из точки B проведем высоту на основание AC в точку H (AC - основание, так как по условию AB = BC). По теореме высота равнобедренного треугольника проведённая к основанию является биссектрисой и медианой, тогда так как по построению BH ⊥ AC, то AH = HC. Рассмотрим прямоугольный треугольник ΔBHC:

$\cos \angle ACB = \dfrac{HC}{BC} \Longrightarrow HC = BC \cdot \cos \angle ACB = a \cos \alpha$.

Так как AH = HC и по основному свойству отрезка:

$AC = AH + HC = 2HC = 2a \cos \alpha$.

По формуле площади треугольника:

$S_{зABC} = \dfrac{AC \cdot BC \cdot \sin \angle ACB}{2} = \dfrac{2a \cos (\alpha) \cdot a \cdot \sin (\alpha )}{2} = a^{2} \cos \alpha \sin \alpha$.

Так как по условию все двугранные пирамиды при рёбрах основания равны β, то по теореме:

$S_{b} = \dfrac{S_{зABC}}{\cos \beta } = \dfrac{a^{2} \cos \alpha \sin \alpha}{\cos \beta }$.

Из точки K проведем перпендикуляр к стороне AB в точку T, то есть

KT ⊥ AB. Соединим точки O и T. Так как по условию OK ⊥ ABC, то по определению прямой перпендикулярной к плоскости KO ⊥ TO, так как TO ⊂ ABC.

По теореме обратной к теореме о трех перпендикулярах OT ⊥ AB, так как  KO ⊥ TO; KT ⊥ AB - по построению и отрезок TO - проекция отрезка KT на плоскость ABC (ΔKOT - прямоугольный, так

как KO ⊥ TO).

Так как OT ⊥ AB и KT ⊥ AB, то угол ∠KTO - линейный угол двугранного угла, то есть ∠(KAB,ABC) = ∠KTO = β.

Так как OT ⊥ AB и по теореме если двугранные углы пирамиды при рёбрах основания равны, то вершина пирамиды проектируется в центр вписанной окружности, то есть точка O - центр вписанной окружности в треугольнике ΔABC, следовательно отрезок OT - радиус вписанной окружности.

Пусть p - полупериметр треугольника ΔABC, тогда по определению полупериметра:

$p = \dfrac{AB + BC + AC}{2} = \dfrac{a + a + 2a \cos \alpha}{2} = \dfrac{2a(1 + \cos \alpha)}{2} = a(1 + \cos \alpha)$.

По формуле площади треугольника:

$S_{зABC} = p\cdot OT \Longrightarrow OT = \dfrac{S_{зABC}}{p} = \dfrac{a^{2} \cos \alpha \sin \alpha}{a(1 + \cos \alpha)} = \dfrac{a \cos \alpha \sin \alpha}{(1 + \cos \alpha)}$.

Рассмотрим прямоугольный треугольник ΔKOT:

$\rm tg \ \beta = \dfrac{OK}{OT} \Longrightarrow OK = OT \cdot tg \ \beta = \dfrac{a \cos \alpha \sin \alpha \ tg \ \beta}{(1 + \cos \alpha)}$.