Question

Дана полуокружность. Найдите геометрическое место середин отрезков, концы которых лежат на этой полуокружности​

Answer 1

Ответ:

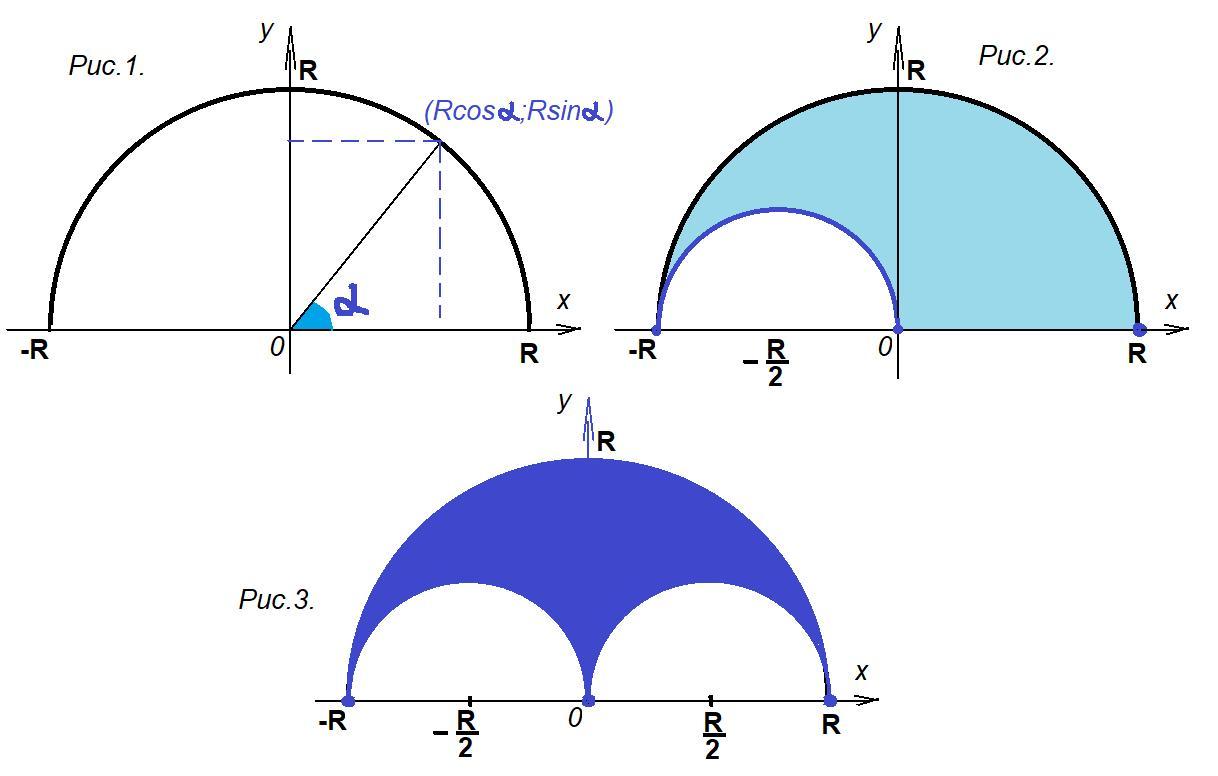
Геометрическое место середин отрезков, концы которых лежат на полуокружности, представлено в приложении на рис. 3.

Пошаговое объяснение:

Пусть дана полуокружность с радиусом R и центром в точке $(0;0)$ (рис. 1.).

Любую точку этой полуокружности можно представить в виде:

$\displaystyle\left \{ {{x=R\cdot \cos \alpha } \atop {y=R\cdot \sin\alpha }} \right. ;\ \ \ \ 0^\circ\le \alpha \le 180^\circ;\ \ \ \ \left \ {{-R\le x\le R} \atop {\ \ \ 0\le y \le R}} \right.$

Максимальная длина отрезка, концы которого лежат на полуокружности, равна диаметру. Середина такого отрезка - это центр полуокружности. Геометрическое место середины отрезка-диаметра в системе координат - это точка  $(0;0).$

Минимальная длина отрезка, концы которого лежат на полуокружности, равна нулю, если концы отрезка совпадают. В этом случае середина отрезка совпадает с концами отрезка. Геометрическое место середин вырожденных отрезков - сама полуокружность.

Середины произвольных отрезков будут находиться в пределах полукруга, ограниченного заданной полуокружностью и осью Ох.

Координаты середины любого отрезка можно посчитать как среднее арифметическое координат концов отрезка:

$x_c=\dfrac{x_1+x_2}2;\ \ \ \ y_c=\dfrac{y_1+y_2}2$

Возьмём две точки полуокружности $(x_1; y_1);\ (x_2; y_2).$ Одна точка произвольная, а вторая находится в первой четверти.

Для координат любых этих точек выполняются условия:

$x_1\ge -R;\ \ \ y_1\ge 0;\\x_2=R\cos\alpha\ge0;\ \ \ y_2=R\sin\alpha\ge 0;\\0^\circ\le\alpha \le 90^\circ$

Тогда для координат середины такого отрезка выполняются неравенства:

$\displaystyle\left \{ {{x_c=\dfrac{x_1+x_2}2\ge\dfrac{-R+R\cos\alpha }2} \atop {y_c=\dfrac{y_1+y_2}2}\ge\dfrac{0+R\sin\alpha }2} \right.$

Преобразуем неравенства:

$\displaystyle\left \{ {{x_c\ge\dfrac{-R+R\cos\alpha }2} \atop {y_c\ge\dfrac{R\sin\alpha }2\ \ \ \ \ } \right.\ \ \ \Leftrightarrow\ \ \ \left \{ {{x_c+\dfrac R2\ge\dfrac R2\cdot \cos\alpha \atop {y_c\ge\dfrac R2\cdot \sin\alpha\ \ \ \ \ } \right.$

В обоих неравенствах правые части неотрицательные, левые не меньше их, то есть тоже неотрицательные. Возведём в квадрат и сложим оба неравенства:

$\displaystyle\left \{ {{\left(x_c+\dfrac R2\right)^2\ge\left(\dfrac R2\right)^2\cdot \cos^2\alpha \atop {y_c^2\ge\left(\dfrac R2\right)^2\cdot \sin^2\alpha\ \ \ \ \ } \right.+\\-----------------\\\left(x_c+\dfrac R2\right)^2+y_c^2\ge\left(\dfrac R2\right)^2\cdot \cos^2\alpha+\left(\dfrac R2\right)^2\cdot \sin^2\alpha\\\\\left(x_c+\dfrac R2\right)^2+y_c^2\ge\left(\dfrac R2\right)^2\cdot \underbrace{\left(\cos^2\alpha+\sin^2\alpha\right)}_{=1}$

$\left(x_c+\dfrac R2\right)^2+y_c^2=\left(\dfrac R2\right)^2$  

Это уравнение окружности с радиусом $\dfrac R2$  и  центром в точке $\left(-\dfrac R2;0\right).$

Тогда точки, удовлетворяющие неравенству:

$\left(x_c+\dfrac R2\right)^2+y_c^2\ge\left(\dfrac R2\right)^2$,  лежат либо на окружности, либо вне круга с радиусом $\dfrac R2$ и центром в точке $\left(-\dfrac R2;0\right).$  Рис. 2.

Так как полуокружность симметрична относительно оси Оу, то в первой четверти можно вырезать точно такую же область, в которую середины отрезков попасть не могут. Эта ситуация соответствует условию, что один конец отрезка находится во второй четверти, а второй конец выбран произвольно. Таким образом, все возможные случаи расположения концов отрезков учтены.

На рис.3 синим цветом показано геометрическое место середин отрезков, концы которых лежат на полуокружности.