Предмет: Алгебра,
автор: mamleeva357
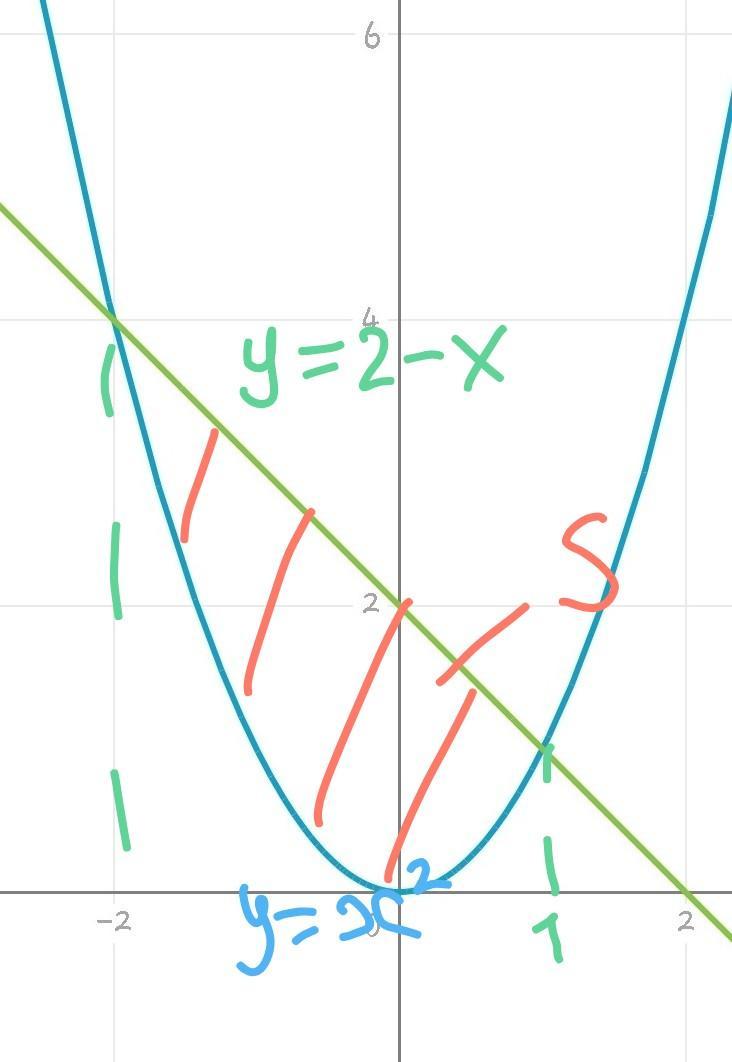
Ребят, помогите найти площадь фигуры, ограниченной линиями. Спасибо!
Дам 30 баллов.
Приложения:

Ответы
Автор ответа:
1
Ответ:
1.
рисунок
2.
Найдем пределы интегрирования:
рисунок2
Приложения:

mamleeva357:
Громадное спасибо, Милая!!!❤️
Похожие вопросы
Предмет: Русский язык,
автор: vacik666
Предмет: Русский язык,
автор: нина211
Предмет: Русский язык,
автор: алина1148
Предмет: Қазақ тiлi,
автор: Аида11111113
Предмет: Математика,
автор: qwertyland0099