Question

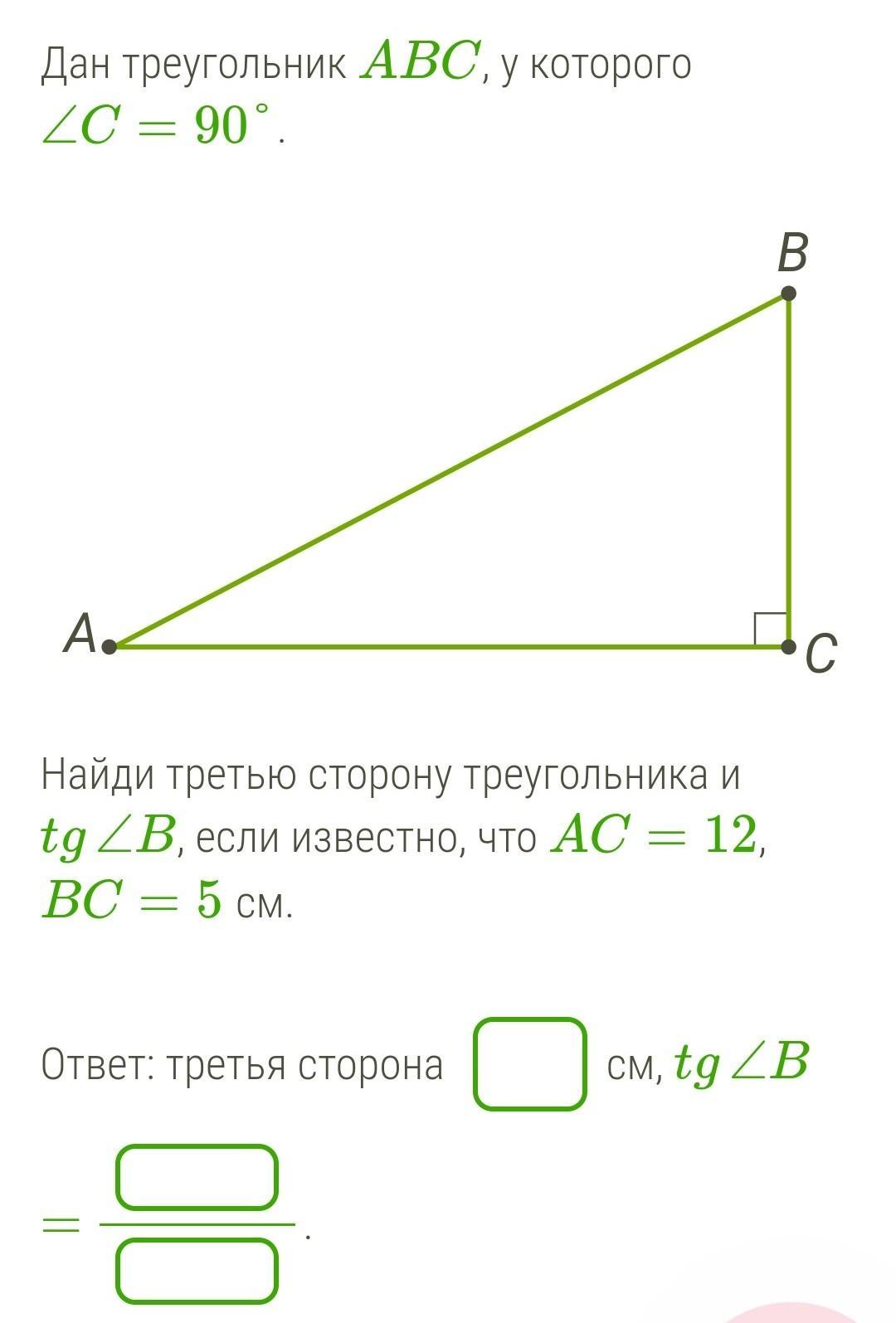
Дан треугольник ABC, у которого ∠C=90°.

Найди третью сторону треугольника и tg∠B, если известно, что AC=12, BC=5 см​

Answer 1

Ответ:

Третья сторона 13 см, tg∠B = $\frac{12}{5}$

Объяснение:

Сначала найдём 3ю сторону по теореме Пифагора a² = b² + c²

АВ² = АС² + ВС²

АВ² = 144 + 25 = 169

АВ = √169 = 13

АВ = 13 см;

Теперь найдём тангенс угла В, напомню, что тангенс это отношение противолежащего катета к прилежащему, если выразить в виде дроби то  $\frac{AC}{BC}$

получается $\frac{12}{5}$ , это и есть тангенс угла В

Answer 2

Ответ:

АВ=13 см;

<В= 2,4.

Объяснение:

1) Найдем третью сторону треугольника АВС с помощью теоремы Пифагора:

с²=а²+b²

АВ²= АС²+ВС²= 5²+12²=25+144= √169=13

АВ=13 см

2) Тангенс острого угла прямоугольного треугольника- это отношение противолежащего катета к прилежащему, значит, тангенс <В = АС/ВС= 12/5=2,4.