Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста, Нужно решить задачу!!
Приложения:
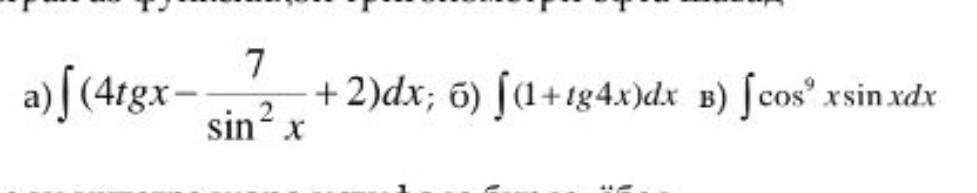
Ответы
Автор ответа:
1
Ответ:
a)
б)
в)
Похожие вопросы
Предмет: Русский язык,
автор: Meruert2005
Предмет: Окружающий мир,
автор: sutyagina76
Предмет: Русский язык,
автор: Koval1984
Предмет: Математика,
автор: So272
Предмет: Математика,
автор: dinbili89