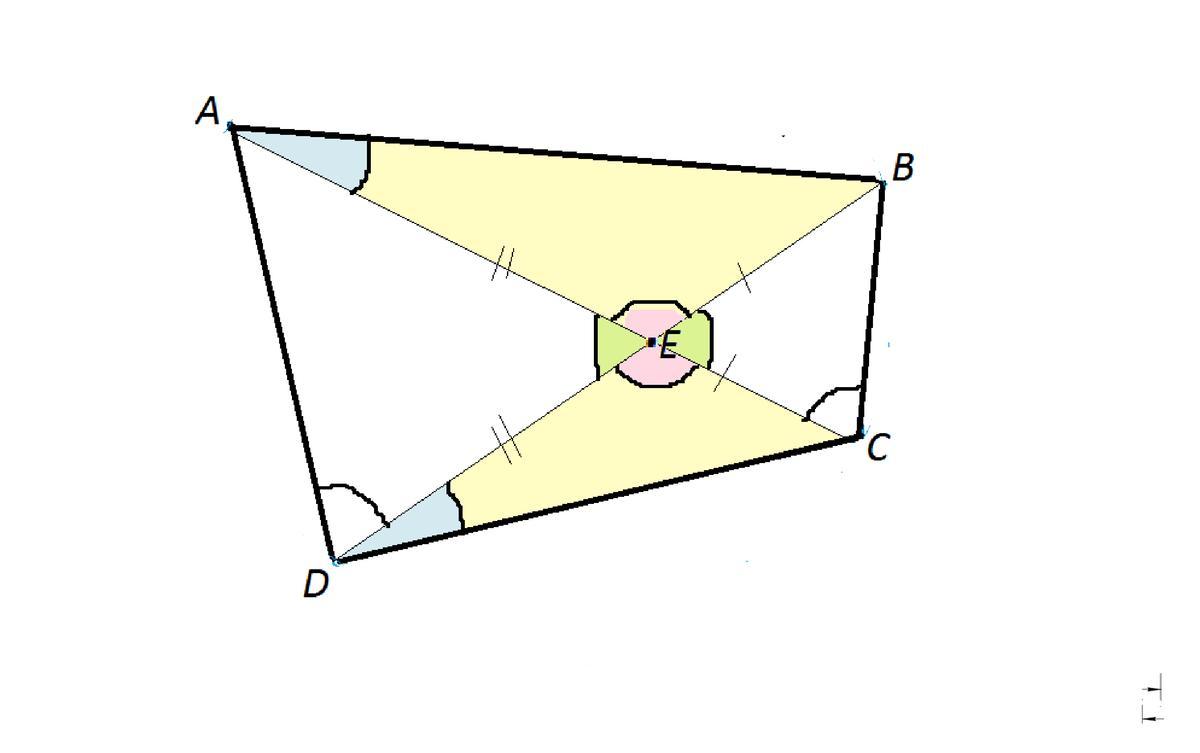
В выпуклом четырёхугольнике ABCD углы CDB и CAB равны. Докажите, что углы BCA u CDB тоже равны.
Вопрос в том, почему из равенства данных в условии задачи углов следует, что около четырёхугольника можно описать окружность?)
Ответы
Объяснение:
Треугольник ADE и BCE подобны и углы, проволежащие пропорционально сторонам, равны =>уголBDA=углуBCA

Ответ:Проведем диагонали АС и ВD.Точку пересечения обозначим Е.
В треугольниках ABE и CDE имеется по два равных угла: один - по
условию, второй - вертикальный.
Первый признак подобия треугольников:
Если два угла одного треугольника соответственно равны двум углам
другого, то такие треугольники подобны.=
∆ ABE=∆ CDE,=
АЕ пропорциональна DE, ВЕ пропорциональна ЕС.
В треугольниках ADE и BCE:
АЕ пропорциональна DE, BE- пропорциональна СЕ, углы АЕD и ВЕС
равны, как вертикальные.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам
другого треугольника и углы, заключенные между этими сторонами,
равны, то такие треугольники подобны.
Треугольники ADE и BCE подобны и углы, противолежащие
пропорциональным сторонам, равны. =BDA=BCA
надеюсь правильно ✅
Объяснение: