Предмет: Математика,
автор: getroit21
Неопределенный интеграл.
Приложения:
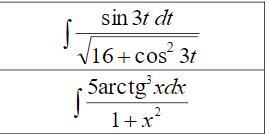
Ответы
Автор ответа:
1
Ответ:
1.
2.
getroit21:
я тебя обожаю
Похожие вопросы
Предмет: Русский язык,
автор: игнат19
Предмет: Українська література,
автор: Kykyryza007
Предмет: Окружающий мир,
автор: marinakapakly86
Предмет: Математика,
автор: vaona
Предмет: Другие предметы,
автор: Suzannas