Предмет: Математика,
автор: akaumov861
Тема: "Дифференциальные уравнения высших порядков, допускающие понижение порядка"
Приложения:
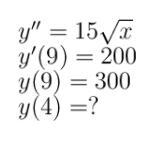
Ответы
Автор ответа:
1
Ответ:
общее решение
частное решение
При х = 4
Ответ: - 194
Похожие вопросы
Предмет: Русский язык,
автор: gulnara6
Предмет: Русский язык,
автор: diana09diana
Предмет: Русский язык,
автор: archideya08
Предмет: Математика,
автор: 110512настя
Предмет: Математика,
автор: Demirlol