Предмет: Математика,
автор: hrapdv358
1. Обчислити визначенні інтеграли та обчислити площу фігури, обмежену лініями.
Приложения:
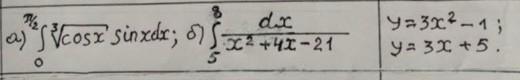


Miroslava227:
второе фото- производная?
Да.
На 3-фото только "а" остальные 4 примера не нужно делать.
Ответы
Автор ответа:
1
1.
2.
3.
Найдем пределы (точки пересечения функций)
рисунок
18.8
а)
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: makcarsakov
Предмет: Русский язык,
автор: ZOOM2006ZOOM
Предмет: Русский язык,
автор: nastya230903
Предмет: Другие предметы,
автор: умница660
Предмет: Английский язык,
автор: гугук