Question

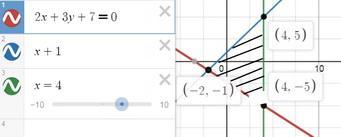
18. Площадь треугольника, образованного прямыми 2х + Зу +7 = 0; у = X + 1; х = 4
равна:​

Answer 1

Даны прямые 2х + Зу +7 = 0; у = х + 1; х = 4.

Находим вершины треугольника.

А: 2х + Зу +7 = 0; у = х + 1, делаем замену :

2х + З(х + 1) = -7,

2х + 3х + 3 = -7,

5х = -10,

х = -10/5 = -2,

2*(-2) + 3у = -7,

у = (-7 + 4) /3 = -1. Точка А(-2; -1).

В. 2х + Зу +7 = 0; х =4, делаем замену :

2*4 + Зу = -7,

3у = -7-8,

3у = -15,

у = -15/3 = -5. Точка В(4; -5).

С. у = х + 1; х = 4. у = 4 + 1 = 5. Точка С(4; 5)

Найдены вершины: А(-2; -1), В(4; -5), С(4; 5).

Площадь треугольника ABC определяем по формуле:      

S=(1/2)*|(Хв-Ха)*(Ус-Уа) - (Хс-Ха)*(Ув-Уа)|.

S = (1/2)*|(4-(-2)*(5*(-1) - (4-(-2)*(-5)*(-1)| = (1/2)*|-30 - 30| = 30 кв.ед.

Ответ: S = 30 кв.ед.

Answer 2

Ответ:

Пошаговое объяснение:

$\displaystyle S= \int\limits^4_{-2} {\bigg ((x+1)- \bigg (-\frac{1}{3} (2x+7)\bigg )\bigg )} \, dx =\frac{1}{3} \int\limits^4_{-2} {(2x+7)x} \, dx +\int\limits^4_{-2} {x} \, dx +\int\limits^4_{-2} {} \, dx =$

$\displaystyle =\frac{5}{3} \int\limits^4_{-2} {x} \, dx +\frac{10}{3} \int\limits^4_{-2} {} \, dx =\bigg (\frac{5x^2}{6} +\frac{10x}{3} \bigg ) \bigg |_{-2}^4=10+20=30$