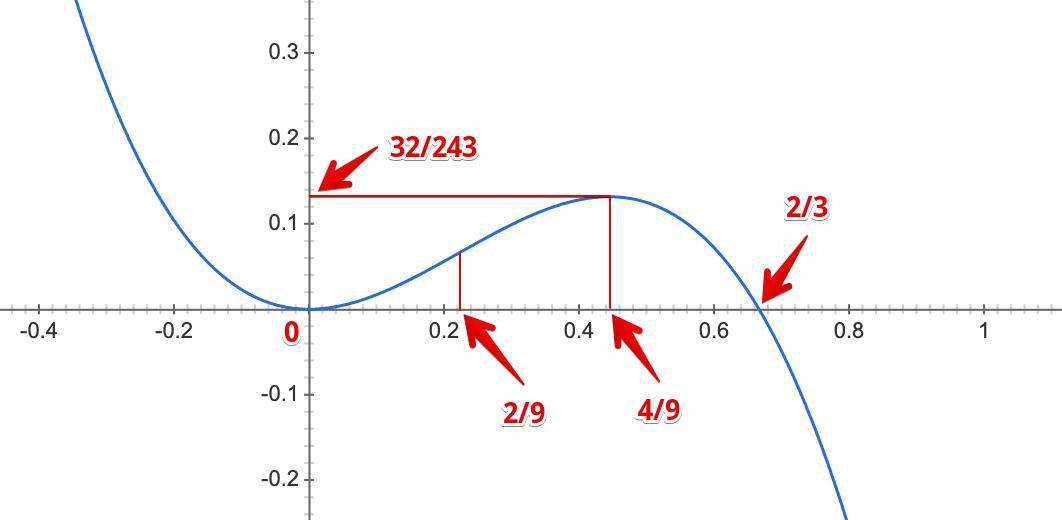
Исследуйте функцию y=f(x) и постройте её график
f(x)=-3x^3+2x^2
Ответы
f(x) = –3x³ + 2x²
1. Области определения и значений
Область определения: x ∈ (–∞; +∞).
Область значений: f(x) ∈ (–∞; +∞).
2. Чётность
f(–x) = –3(–x)³ + 2(–x)² = 3x³ + 2x²
Функция не является ни чётной, ни нечётной.
3. Пересечения с осью OX (корни)
–3x³ + 2x² = 0 ⇔ x²(–3x + 2) = 0
x₁ = 0, x₂ = 2/3
4. Пересечение с осью OY
f(0) = –3·0³ + 2·0² = 0
5. Экстремумы и интервалы монотонности
f'(x) = (–3x³ + 2x²)' = –9x² + 4x = x(–9x + 4)
f'(x) = 0 ⇒ x₁ = 0, x₂ = 4/9
Функция f(x) убывает на интервале (–∞; 0) ∪ (4/9; +∞).
Функция f(x) возрастает на интервале (0; 4/9).
Локальный минимум: x = 0, f(0) = 0.
Локальный максимум: x = 4/9, f(4/9) = –3(4/9)³ + 2(4/9)² = 32/243 ≈ 0,13
6. Выпуклость
f''(x) = (–9x² + 4x)' = –18x + 4
f''(x) = 0 ⇒ x = 2/9
Точка перегиба: x = 2/9.
Функция f(x) вогнутая на интервале (–∞; 2/9).
Функция f(x) выпуклая на интервале (2/9; +∞).