Предмет: Математика,
автор: zhankalybaktybaev16
Ответте на вопрос не скопируй от предыдущего ответа,
(если не правилно тому бан)!
Приложения:
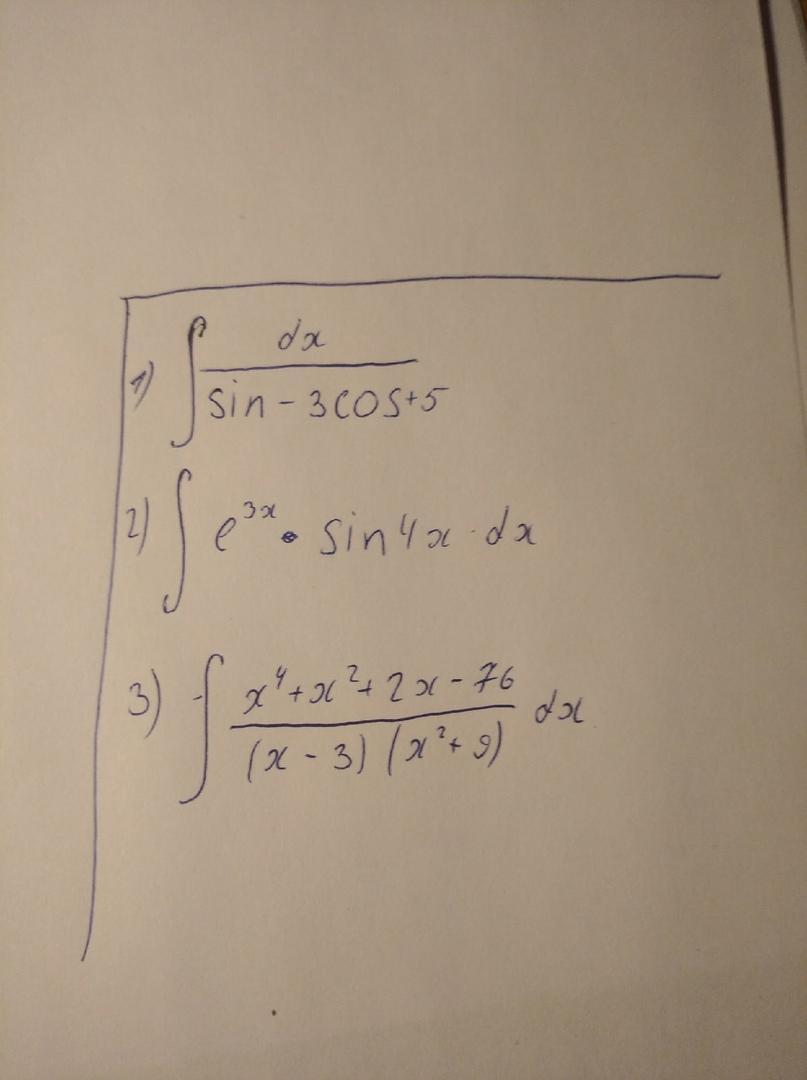
zhankalybaktybaev16:
Помогите пожалуйста!
Если не правилно!
Miroslava227 помогите!
Iife20 помогите!
crazyNick помогите
msby80 помогите!
moonsoull помогите!
От предыдущего нельзя мне дать это ответ неверный!
Ответы
Автор ответа:
6
Пошаговое объяснение:
1.
Тригонометрическая замена:
2.
Интеграл с реккурентной формой.
Решим по частям:
Получили исходный интеграл
Возьмём его за I
Тогда:
Ответ:
3.
Дробь неправильная, выделим целую часть:
С помощью неопределенных коэффициентов:
Получаем:
Ответ:
Вам Большое спасибо!
Похожие вопросы
Предмет: Черчение,
автор: igorswiter
Предмет: Русский язык,
автор: татутуся
Предмет: Английский язык,
автор: iradasha68
Предмет: Французский язык,
автор: PeChEnKa1357
Предмет: Беларуская мова,
автор: ViktoryaWeber