Предмет: Алгебра,
автор: Tamara020971
Очень СРОЧНО!!!!Помогите пожалуйста!!! Срочно!!!
Пожалуйста,если Вас не затруднит , с подробным решением.
Заранее Вам спасибо!!!!
Приложения:
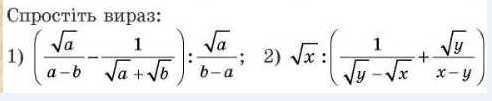
Ответы
Автор ответа:
1
Решение на фото/////
Приложения:

Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Даша05221
Предмет: Русский язык,
автор: Рыжий125
Предмет: Английский язык,
автор: lemon9884
Предмет: Биология,
автор: lenwir
Предмет: Русский язык,
автор: ReGiNoChKa171