Предмет: Алгебра,
автор: ksenia123tea
помогите!! если лень решать, натолкните хотя бы на мысль
Приложения:
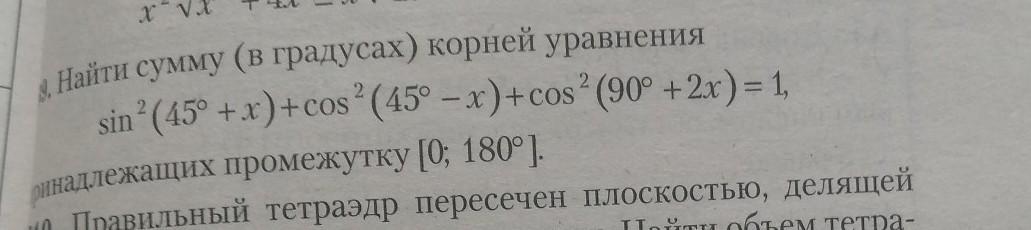
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Окружающий мир,
автор: klimontovich
Предмет: Английский язык,
автор: vicktbarisckay
Предмет: Русский язык,
автор: NLO111
Предмет: Қазақ тiлi,
автор: valeramikheev
Предмет: Математика,
автор: дианамаксим