Question

1. Окружность радиуса 2 см внешне касается другой окружности в
точке А. Общая касательная двух окружностей, проведенная
через точку А, пересекается с другой их общей касательной в
точке В. Найдите радиус другой окружности, если длина отрез-
ка АВ равна 4 см.​

Answer 1

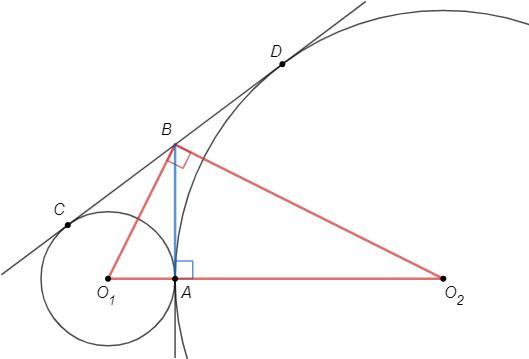
Точка касания двух окружностей (A) лежит на линии центров (O1O2)

Радиус в точку касания перпендикулярен касательной => O1O2⊥BA

По теореме об отрезках касательных из одной точки

BO1 - биссектриса ∠ABC, BO2 - биссектриса ∠ABD

(Док-во: △O1CB=△O1AB по катету (радиусы) и общей гипотенузе)

Биссектрисы смежных углов перпендикулярны, ∠O1BO2=90

BA - высота из прямого угла в △O1BO2

BA^2 =O1A*O2A => O2A =16/2 =8 (см)