Предмет: Алгебра,
автор: Аноним
АЛГЕБРА! Задача! Люди добрі, ДОПОМОЖІТЬ будь ласочка, дуже сильно прошу Вас(((
Приложения:

Ответы
Автор ответа:
1
Ответ:
S =
Объяснение:
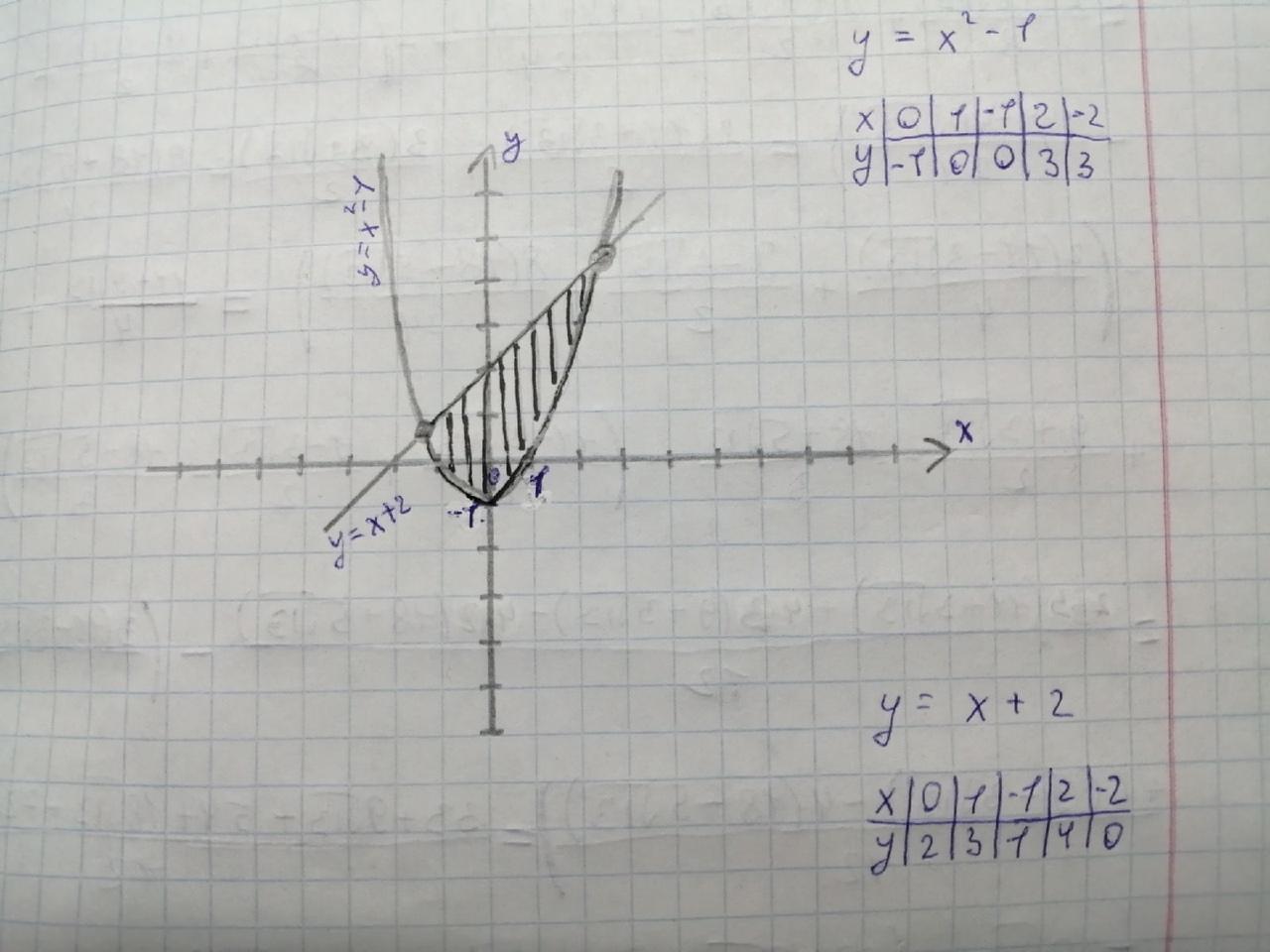
Для решения задачи в первую очередь нужно построить график.
По графику видно, что найти нам нужно площадь области, лежащей над параболой y = x²-1 и под прямой y = x+2.
Найдём точки пересечения данных кривых. Для этого нужно решить систему из уравнений их функций.
Найти площадь фигуры, ограниченной сверху графиком функции y = x+2, а снизу функцией y = x²-1, а так же прямыми x₁ = и x₂ =
, значит вычислить следующий определённый интеграл.
Пока найдём интеграл
Подставим пределы интегрирования
Ответ: (кв. ед.)
фото (график и решение с пределами интеграла)
Приложения:
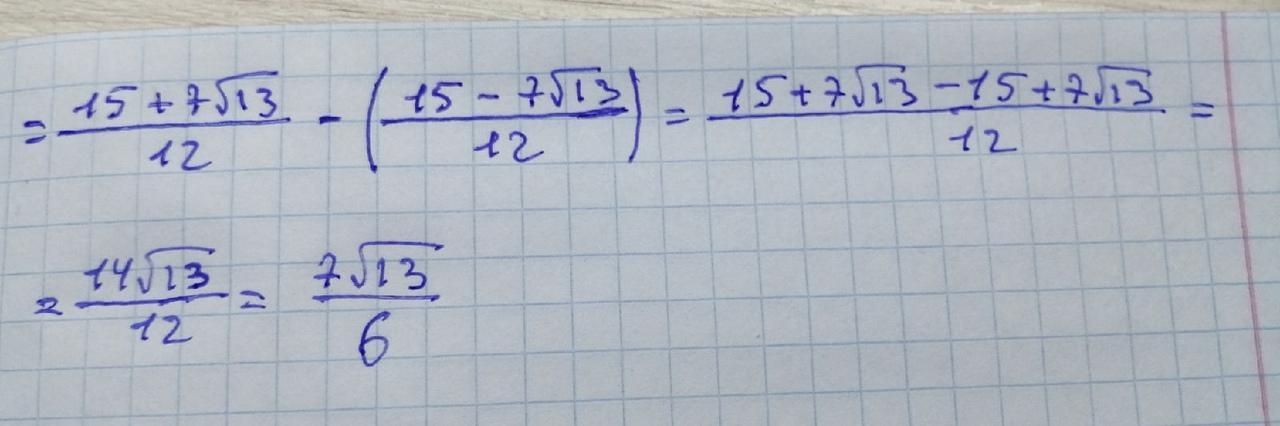

Похожие вопросы
Предмет: Окружающий мир,
автор: юлия050284
Предмет: Русский язык,
автор: дилшод1
Предмет: Окружающий мир,
автор: ЛенаБукатова
Предмет: Литература,
автор: Даша020705
Предмет: Другие предметы,
автор: lyubovbuzuk87