Предмет: Алгебра,
автор: chaneloberlinbts
Решите, пожалуйста!!!
Приложения:
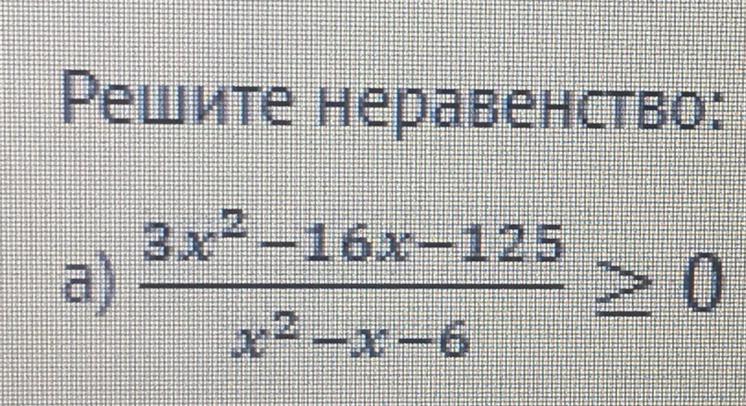
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Українська література,
автор: hjgyt
Предмет: Русский язык,
автор: Кукарикук
Предмет: Українська література,
автор: vlada11187
Предмет: Английский язык,
автор: Оля090073
Предмет: Русский язык,
автор: Аноним