Предмет: Геометрия,
автор: nikakarakonstantin67
Основы равнобедренной трапеции равны 4 см и 16 см. Чему равна площадь данной трапеции, если в нее можно вписать окружность.
Ответы
Автор ответа:
0
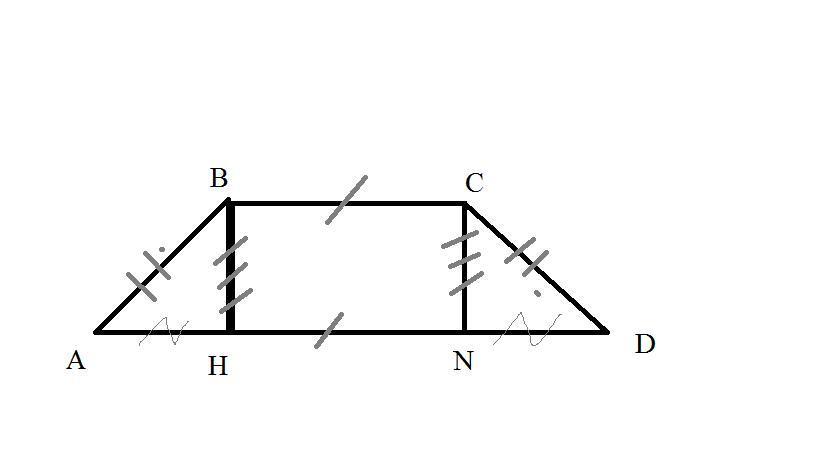
Если в трапецию можно вписать окружность,то её сумма основ равна сумме боковых сторон.
Тогда сумма боковых сторон(AB+CD) равна 20см,а т.к. трапеция равнобедренная,то одна сторона(AB) равна 20:2= 10 см.
Проведём с точек B и C перпендикуляры на основу AD и пусть BH и CN - высоты.
Отрезок AH равен DN,так как высоты,боковые стороны и углы между ними равны ( равность треугольников за 2-мя сторонами и углом между ними).
получаем формулу:
AH = (AD-BC)/2.
AH= 12/2= 6см
Рассмотрим треугольник AHB - прямоугольный
За теоремой Пифагора: BH^2=AB^2-AH^2
BH^2 = 100-36=64
BH=8см
S= (AD-BC)*BH/2= 12*8/2=48 см^2
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: bonbonsveet
Предмет: Қазақ тiлi,
автор: ksyusha123456789010
Предмет: Русский язык,
автор: РинаПаленкова666
Предмет: Русский язык,
автор: solnsze82
Предмет: Физика,
автор: tankor2005