Предмет: Геометрия,
автор: Аноним
геометрия плиззз.......
Приложения:
Ответы
Автор ответа:
0
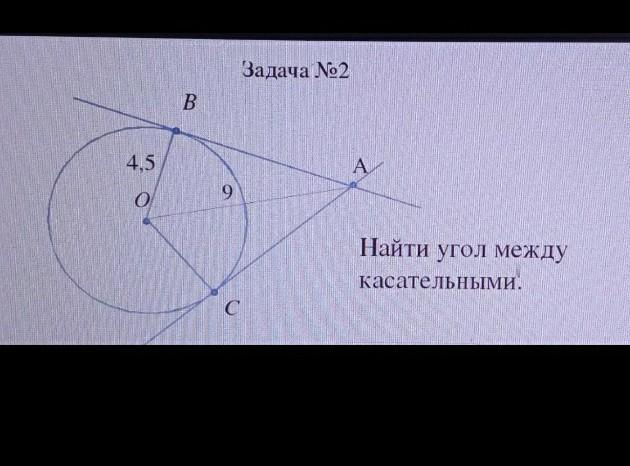
Ответ:ОВ-радиус и перпендикуляр к касательной,образует с ней прямой угол
<ОВА =90 градусов,а это значит,что треугольник ОВА является прямоугольным,где ОВ катет ,а ОА гипотенуза,разница в размерах между гипотенузой и катетом 2
9:4,5=2
Следовательно,катет ОВ лежит против угла З0 градусов
<ВАО=30 градусов
Тоже самое и с треугольником АОС
Радиус ОС перпендикуляр к касательной АС,поэтому
<ОСА=90 градусов и треугольник прямоугольный
Треугольники АОС и ОВА равны между собой по 5 признаку равенства прямоугольных треугольников-по гипотенузе и катетам
ВО=ОС,как радиусы
ОА-общая сторона и гипотенуза
Поэтому
<ВАО=<ОАС=30 градусов
<ВАС=30•2=60 градусов
<ВОА=<СОА=90-30=60 градусов
<ВОС=60•2=120 градусов
Объяснение:
Похожие вопросы
Предмет: Окружающий мир,
автор: oxana116
Предмет: Английский язык,
автор: милафка4
Предмет: Русский язык,
автор: юля900
Предмет: Окружающий мир,
автор: maygaker
Предмет: Русский язык,
автор: Рнпннм