Предмет: Математика,
автор: an6906529
ДАЮ 40 БАЛОВ СРОЧНО РЕШИТЕ!!!!!
Приложения:
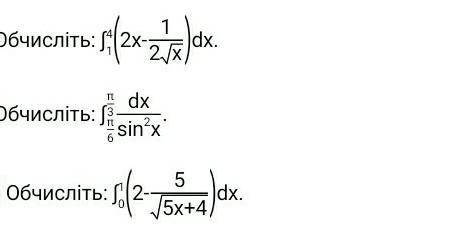
Ответы
Автор ответа:
1
1.
2.
3.
an6906529:
огромное тебе спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: CocaColla200000
Предмет: Русский язык,
автор: Xande
Предмет: Математика,
автор: annafilcenko2281
Предмет: Русский язык,
автор: Аноним