Предмет: Математика,
автор: karevaev63
СРОЧНО ПОМОГИТЕ, ПРОФИЛЬНАЯ МАТЕМАТИКА ПРОШУ
Приложения:

Ответы
Автор ответа:
1
Ответ:
нет корней
n принадлежит Z.
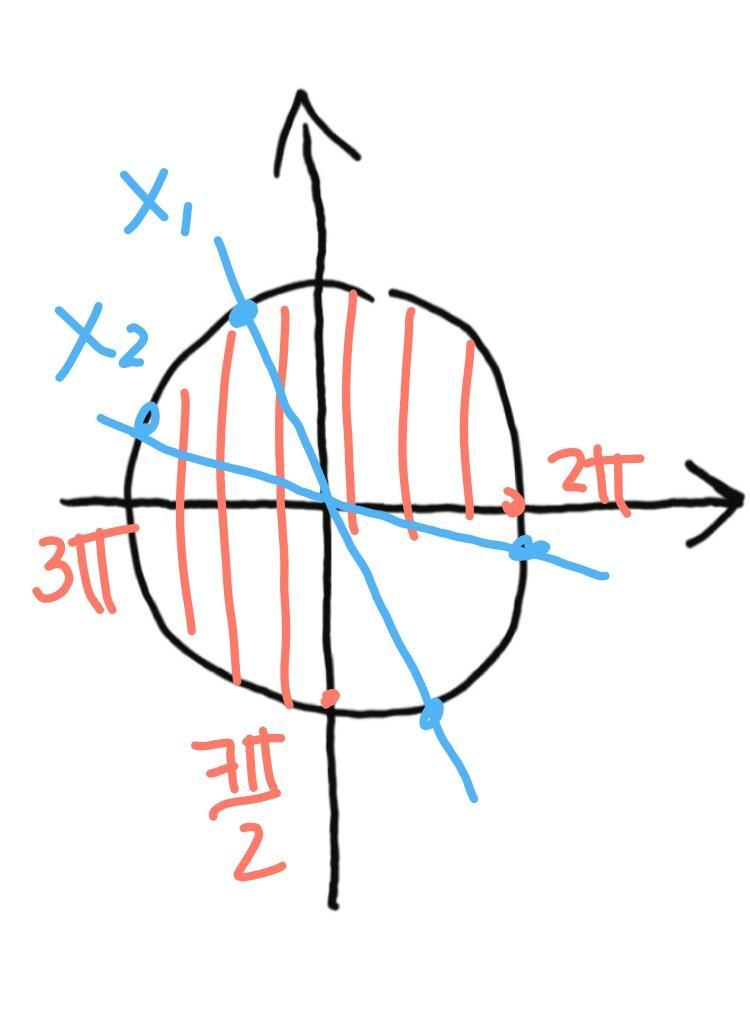
На промежутке:
рисунок:
Ответ:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Vanyalime
Предмет: Русский язык,
автор: 79081240445
Предмет: Русский язык,
автор: ninatkalenko
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: bulatovbulat034