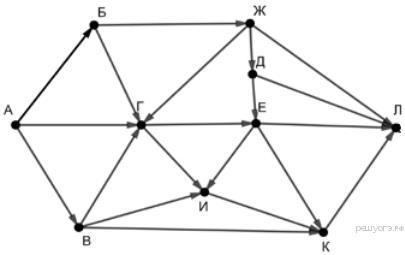
На рисунке — схема дорог, связывающих города
А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно
двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей
из пункта А в пункт Л?
Ответы
Решим эмпирически. В качестве языка будет использован Haskell.
Опишем дороги следующим образом:
- ways = f <$>
- [('A', "BCD"), -- А
- ('B', "DJ"), -- Б
- ('C', "DHI"), -- В
- ('D', "FH"), -- Г
- ('E', "FK"), -- Д
- ('F', "HIK"), -- Е
- ('J', "EK"), -- Ж
- ('H', "I"), -- И
- ('I', "K"), -- К
- ('K', "")] -- Л
- where
- f = second (fmap (, Just 1))
Опишем функции fromA для получения всех возможных путей из заданной начальной точки и функцию findWays для поиска путей из пункта A в пункт B.
- fromA :: Char -> [(Char, Maybe Int)]
- fromA a = join [x | (c, x) <- ways, c == a]
- findWays :: Char -> Char -> [(String, Int)]
- findWays a b = findWays' a b ("", 0)
- findWays' :: Char -> Char -> (String, Int) -> [(String, Int)]
- findWays' a b (w, c)
- | a == b = [(w ++ [a], c)]
- | otherwise = [(w', c'') | (a', Just c') <- fromA a, a' `notElem` w, (w', c'') <- findWays' a' b (w ++ [a], c + c')]
В findWays передаются начальная и конечная точки маршрута, для начальной точки ищутся все возможные пути, затем для каждого из таких путей мы ищем новые пути и так далее до тех пор, пока начальная и конечные точки в вызове функции не будут совпадать.
Результат вызова для findWays 'A' 'K':
[("ABDFHIK",6),("ABDFIK",5),("ABDFK",4),("ABDHIK",5),("ABJEFHIK",7),("ABJEFIK",6),("ABJEFK",5),("ABJEK",4),("ABJK",3),("ACDFHIK",6),("ACDFIK",5),("ACDFK",4),("ACDHIK",5),("ACHIK",4),("ACIK",3),("ADFHIK",5),("ADFIK",4),("ADFK",3),("ADHIK",4)]
Это все пути, ведущие из города 'A' в город 'K' (для простоты названия городов были заменены на английские, правило замены приведено выше)
Чтобы найти количество, а не сами маршруты достаточно выполнить length $ findWays 'A' 'K': 19.
Ответ: 19 путей существует из города A в город Л.