Предмет: Геометрия,
автор: tamilla91
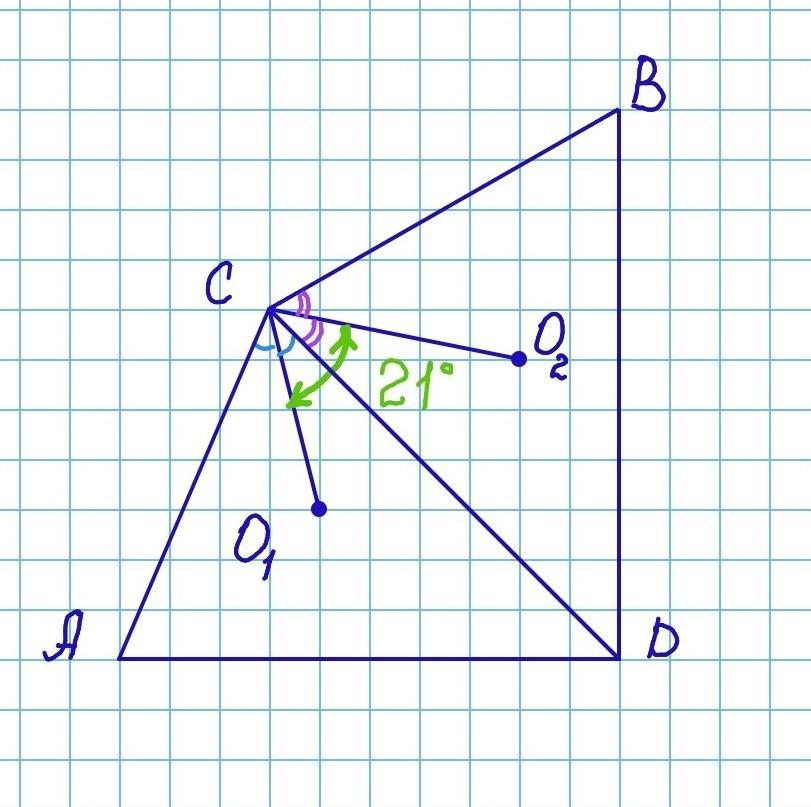
На рисунке O1 и O2 – центры вписанных окружностей в треугольники ADC и DBC соответственно. Найди угол ACB, если ∠O1CO2 = 21°.
Ответы
Автор ответа:
0
Ответ:
Угол ACB равен 42°
Объяснение:
Известно, что центр вписанной в треугольник окружности лежит на пересечении его биссектрис.
Поэтому СО1 - биссектриса ∠AСD, а СО2 - биссектриса ∠BCD: ∠CO1=∠DCO1, ∠BCO2=∠DCO2.
Таким образом ∠AСD = 2•∠DСО1, а ∠BCD = 2•∠DCO2
∠ACB=∠AСD+∠BCD=2•∠DСО1+2•∠DCO2=2•(∠ DСО1+∠DCO2)=2•∠O1CO2=2•21°=42°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: бекишева
Предмет: Английский язык,
автор: armingahrorahma
Предмет: Французский язык,
автор: paxan7
Предмет: Математика,
автор: adiasharipova2004
Предмет: Немецкий язык,
автор: Анастасия9497