Предмет: Алгебра,
автор: step2106s
* РЕШИТЕ! 50 БАЛЛОВ !*
Приложения:
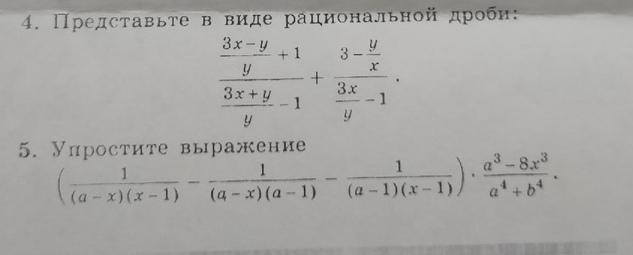
Ответы
Автор ответа:
0
Ответ:
NNNLLL54:
а слова поганые можно не писать ???
Похожие вопросы
Предмет: Русский язык,
автор: алена2932
Предмет: Окружающий мир,
автор: Аноним
Предмет: Английский язык,
автор: oksi666ksi
Предмет: Алгебра,
автор: NikitosMir
Предмет: Литература,
автор: звездопад02