Предмет: Математика,
автор: angelina745547
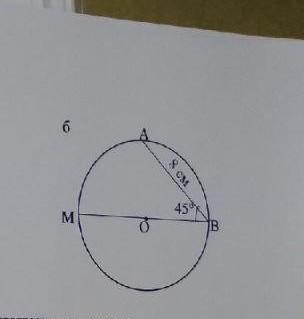
найти расстояние от точки М до прямой ав ПОЖАЛУЙСТА ДАМ 20 БАЛЛОВ
Приложения:
Ответы
Автор ответа:
1
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
У нас получился прямоугольний треугольник
отсюда
(см).
Приложения:
Автор ответа:
0
Ответ:
8
Пошаговое объяснение:
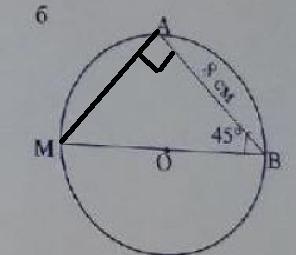
достроим MA, треугольник MAB - прямоугольный и равнобедренный, т.к. угол MAB опирается на диаметр, то он равен 90 градусов. Из треугольника MAB, MA=AB=8, т.к. треугольник равнобедренный, по т. пифагора =
= 64 + 64 = 8
. Проведём высоту MH к стороне AB. Рассмотрим треугольник MHB. синус угла HBM =
MH = * 8
( т.к. синус 45 =
) = 8
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: FIt11
Предмет: Қазақ тiлi,
автор: bibka2
Предмет: Русский язык,
автор: ника272
Предмет: Алгебра,
автор: arturkrishchyan