Предмет: Математика,
автор: bibose
найти производную..
Приложения:
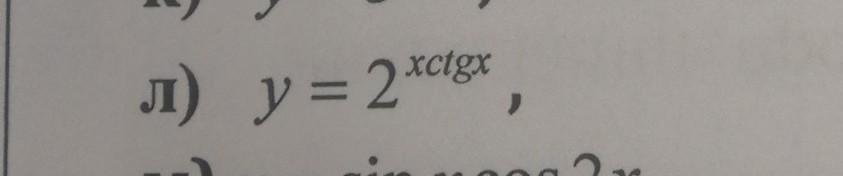
Ответы
Автор ответа:
1
Мы имеем дело с производной сложной функции: у' = (2^(x·ctgx))' = 2^(x·ctgx) · ㏑2 · (x·ctgx)' = 2^(x·ctgx) · ㏑2 · (1·ctgx + x · (-1/sin²x)) =
2^(x·ctgx) · (ctgx - x/sin²x) · ㏑2
б) пусть у = 3^(-x²), тогда y' = 3^(-x²) · ㏑3 · (-2x)
amanda2sempl:
пусть у = 3^(-x²), тогда y' = 3^(-x²) · ㏑3 · (-2x)
Похожие вопросы
Предмет: Русский язык,
автор: olegdyubanok
Предмет: Русский язык,
автор: gimginaira
Предмет: Окружающий мир,
автор: КУРЛЫК555
Предмет: Математика,
автор: даша22011
Предмет: Геометрия,
автор: БольшойДжонни