Дана трапеция ABCDABCD с основанием ADAD, в которой выполнены равенства AB=BCAB=BC, AC=CDAC=CD, BC+CD=ADBC+CD=AD. Найдите величину наибольшего угла трапеции ABCDABCD.
Ответы
Дана трапеция ABCD с основанием AD, в которой выполнены равенства AB=BC, AC=CD, BC+CD=AD. Найдите величину наибольшего угла трапеции ABCD.
Ответ:
Величина наибольшего угла трапеции ABCD: ∠С=144°.
Объяснение:
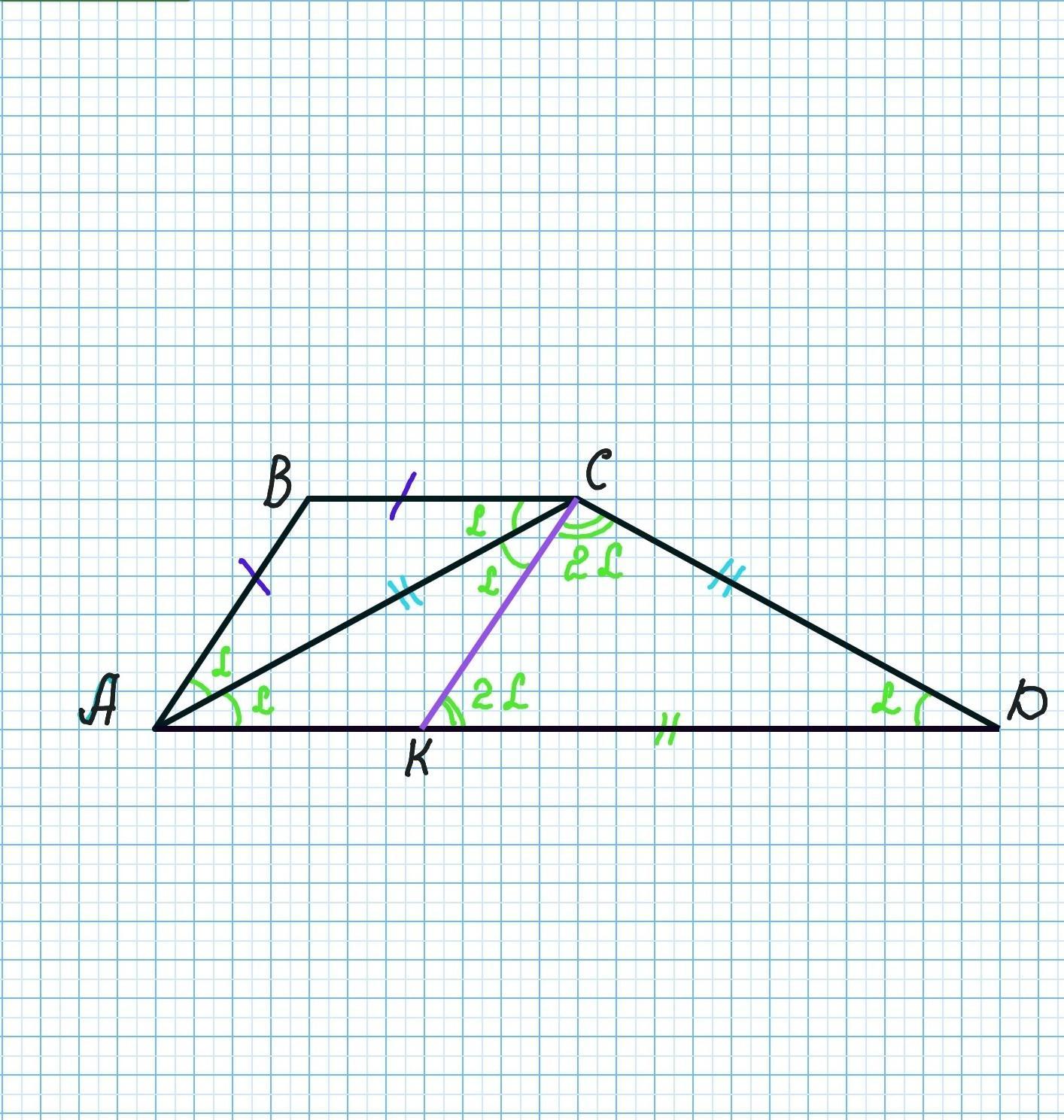
Сделаем дополнительные построения. Проведём СК ІІ АВ.
ВС II AK - как основания трапеции, СК ІІ АВ - по построению, => АВСК - параллелограмм.
АВ=ВС - по условию, АВ=СК, ВС=АК - как стороны параллелограмма (AB=BC=CK=AK) => АВСК - ромб.
- Параллелограмм, у которого все стороны равны является ромбом.
Диагональ ромба является биссектрисой его углов.
Пусть ∠СAВ=∠CAK=∠ACB=∠ACK=α. Тогда ∠СКD=∠BCK=2α - как внутренние накрест лежащие углы, образованные при пересечении параллельных прямых ВС и AD секущей CK.
Так как AC=CD, то △AСD - равнобедренный, а у равнобедренного треугольника углы при основании равны: ∠CDK =∠CAD = α.
Из условия нам известно: BC+CD=AD, но ВС=АК, как стороны ромба, а AD= AK+KD, следовательно перепишем наше равенство следующим образом:
АК+CD=AK+KD.
CD=KD
СD и KD являются боковыми сторонами △СDК. Следовательно △СDК - равнобедренный. По свойству равнобедренного треугольника: ∠DCK=∠DKC=2α.
Так как сумма углов треугольника равна 180°, то:
∠CKD+∠DCK+∠CDK=180°,
2α+2α+α=180°
5α=180°,
α=36°.
Рассмотрим углы трапеции ABCD.
∠D=α=36°,
∠A=2α=2×36°=72°.
Так как сумма углов трапеции, прилегающих к боковой стороне равна 180°, то:
∠B=180°-∠A=180°-72°=108°,
∠C=180°-∠D=180°-36°=144°.
Итак, наибольший угол трапеции равен 144°.