Предмет: Математика,
автор: meinshel4511
Помогите решить, пожалуйста
Приложения:
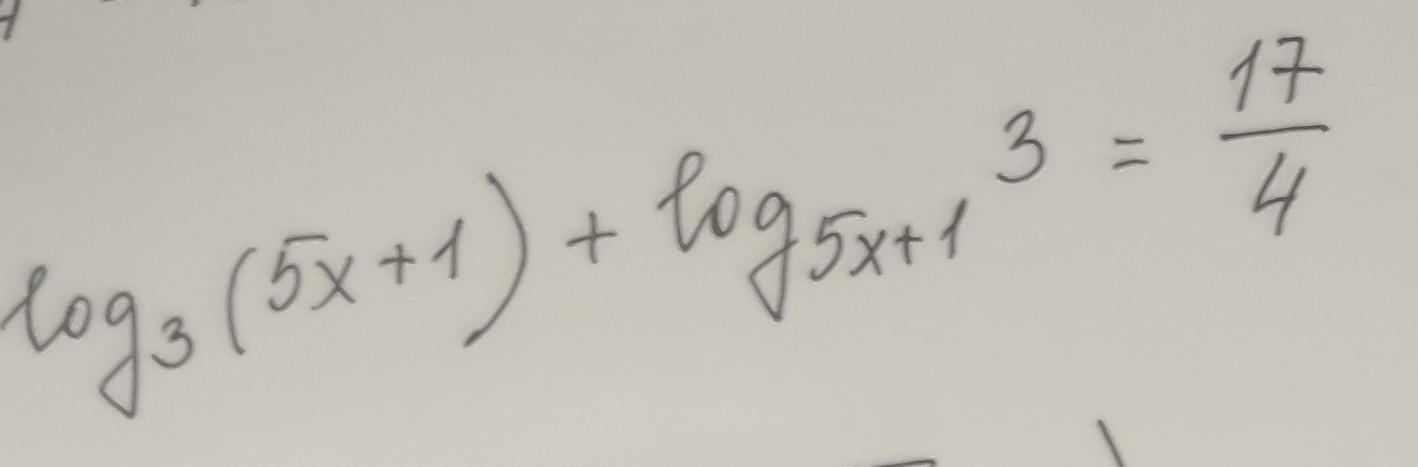
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: надя119
Предмет: Русский язык,
автор: паника2
Предмет: Математика,
автор: Аноним