Предмет: Математика,
автор: aniytik2003
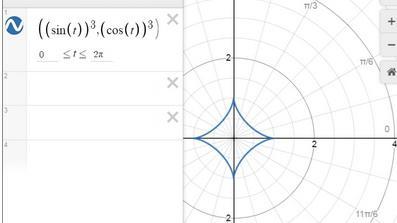
1) Обчислити площу фігури, що обмежена лінією {x=cos^3t яка задана параметрично.
{y=sin^3t ,
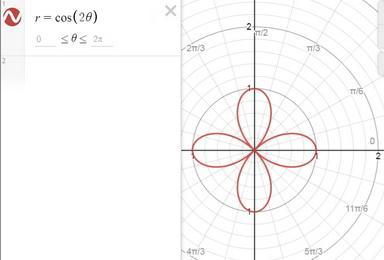
2) Обчислити площу фігури, що обмежена лінією p= cos*2φ в полярній системі координат.
Приложения:

Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
5)
это параметрическое уравнение астроиды
тут заморачиваться не надо, есть формула для расчета площади астроиды
у нас a = b = 1
поэтому наша площадь будет равна
S = 3π /8
6) здесь у нас полярная роза с 4 лепестками.
один лепесток можно было бы просто посчитать от 0 до п/2, но мы уже посчитаем как положено от -п/4 до п/4 (это абсолютно равноплощадно)
площадь одного лепестка считаем по формуле площади криволинейного сектора
и тогда искомая полощадь
S = п/8 *4 = п/2
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: PODSHIVALOVA82
Предмет: Русский язык,
автор: КоцерубоНиколай
Предмет: Английский язык,
автор: вика446
Предмет: История,
автор: Лицеисткрут
Предмет: Математика,
автор: naste15