Question

Решение задач Помогите по братский

Answer 1

Ответ:

Ответ:номер 1

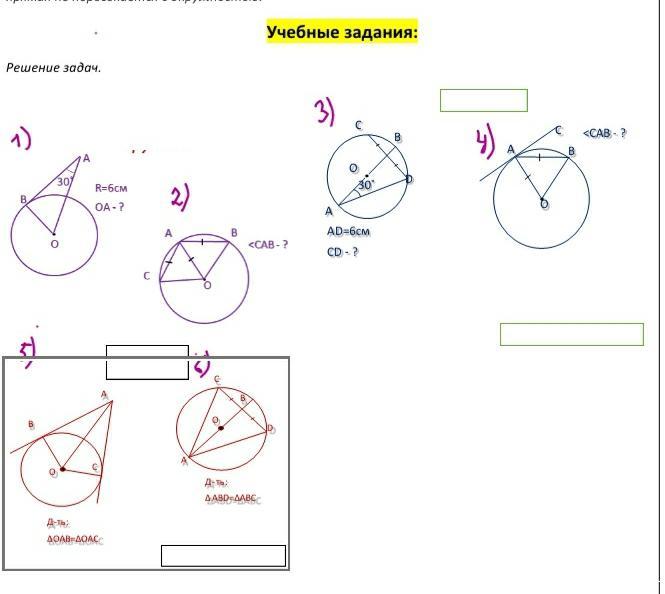
ОВ=6 см,т к это радиус

Радиус ОВ и секущая ВА образуют < 90 градусов, т к ОВ перпендикуляр к ВА,из этого вывод- треугольник АОВ прямоугольный,катет ОВ лежит против угла 30 градусов,значит гипотенуза АО в два раза больше катета

АО=6•2=12 см

Номер 2

По условию задачи

СА=АО=АВ ,НО

АО=СО=ОВ как радиусы,тогда

СА=АО=АВ=СО=ОВ

И из этого сокет,что

треугольник САО равен треугольнику АОВ и они являются равносторонними-их стороны равны и каждый угол равен 60 градусов

<САВ=<САО+<ОАВ=60+60=120 градусов

Номер 3

В1D находится против угла 30 градусов и вдвое меньше гипотенузы АD

B1D=6:2=3 cм

СD=B1D+B1C=3•2=6 cм

Номер 4

АО=AB по условию задачи ,НО

АО=ОВ , как радиусы. , тогда

АО=АВ=ОВ треугольник равносторонний и равноугольный,каждый угол равен по 60 градусов

<ОАВ=60 градусов

Тут пересекается секущая АС с радиусом АО,который является перпендикуляром к секущей,поэтому угол ОАС равен 90 градусов

<САВ=90-60=30 градусов

Номер 5

ВО перпендикуляр к секущей АВ

ОС перпендикуляр к секущей ОС,тогда

<АВО=<АСО=90 градусов,значит треугольники прямоугольные

АО-общая и гипотенуза

ВО=ОС,как радиусы и это катеты

Треугольники равны по 5 признаку равенства прямоугольных треугольников-по катету и гипотенузе

Номер 6

Треугольники равны по 1 признаку равенства треугольников-по двум катетам

АВ-общая сторона и катет

СВ=ВО по условию задачи

Объяснение: