Question

1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

Answer 1

При периметре 45 см сторона  правильного треугольника 45:3=15 см

Формула радиуса описанной окружности около правильного треугольника

R=a/√3 => R=15/√3=5√3 

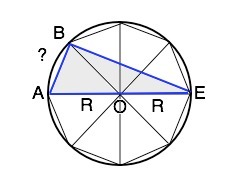
Соединив вершину В вписанного восьмиугольника с концами диаметра  АЕ описанной окружности, получим ∆ АВЕ. 

Угол АОВ=360°:8=45°

Вписанный угол ВЕА=22,5°

По т.синусов АЕ=2R=АВ:sin22,5° =>

АВ=2R•sin22,5=10√3•0,38268=6,628 см

———————

Сторону вписанного n- угольника можно найти из Формулы радиуса описанной  окружности  правильного  многоугольника

$R= frac{a}{2sin frac{180^o}{N} }$ где N- количество сторон многоугольника.