Предмет: Математика,
автор: yarsbot2
Решите диф. уравнение
Приложения:
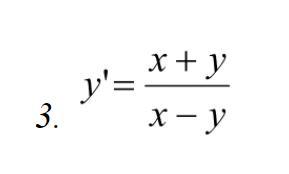
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: blondie4137
Предмет: Русский язык,
автор: ксюняksu
Предмет: Английский язык,
автор: яро23
Предмет: Русский язык,
автор: HIERA2000
Предмет: Русский язык,
автор: trixi1989vv