Предмет: Алгебра,
автор: xDanielAngelx
Найдите производную функцию
Приложения:
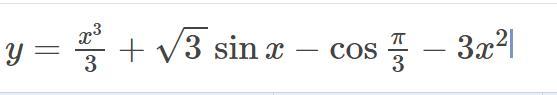
Ответы
Автор ответа:
1
Ответ:
Объяснение:
xDanielAngelx:
Математик лучший))
Похожие вопросы
Предмет: Немецкий язык,
автор: megabambur2000
Предмет: Русский язык,
автор: Соня56655
Предмет: Русский язык,
автор: Артём65
Предмет: Русский язык,
автор: Аноним