Предмет: Алгебра,
автор: xDanielAngelx
Найдите угловой коэффициент касательной проведенной к графику функции f в точке с абсциссой x0
Пример:
1)Фото
2)x0=625
P.S х в нулевом степени
Приложения:
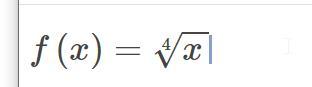
Ответы
Автор ответа:
1
Ответ:
Объяснение:
xDanielAngelx:
Математик спасибо))
Похожие вопросы
Предмет: Английский язык,
автор: ArtemIwashkowih
Предмет: Русский язык,
автор: linaserga
Предмет: Английский язык,
автор: Sokol5667
Предмет: Математика,
автор: bugi2005
Предмет: История,
автор: PAX123er3q4