Предмет: Математика,
автор: ninavictoria
Натуральные числа нужно решение срочьно
Приложения:
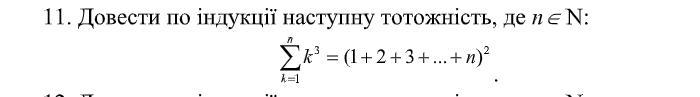
Ответы
Автор ответа:
1
Пошаговое объяснение:
Если простым языком, то нам надо доказать что 1³+2³+3³+...+n³=(1+2+3+...+n)²
1)База(для n=1):
1³=1²⇒1=1 верно
2)Допустим для n=k выполняется; имеем:
1³+2³+3³+...+k³=(1+2+3+...+k)²
3)Докажем что выполняется для n=k+1 следующее:
1³+2³+3³+...+k³+(k+1)³=(1+2+3+...+k+(k+1))²
Доказательство:
1³+2³+3³+...+k³+(k+1)³=(1+2+3+...+k)²+(k+1)³=(1+2+3+...+k)²+2k(k+1)÷2×(k+1)+(k+1)²
Т.к. 1+2+3+...+n=n(n+1)÷2 (данное равенство доказывается отдельно индукцией), имеем:
1³+2³+3³+...+(k+1)³=(1+2+3+...+(k+1))², т.е. утверждение верно при n=k+1.
Таким образом, сумма кубов n последовательных чисел от 1 до n равна квадрату суммы последовательных чисел от 1 до n, что и требовалось доказать Δ
Похожие вопросы
Предмет: Русский язык,
автор: Vadimjdjskks
Предмет: Русский язык,
автор: Anastasia17062004
Предмет: Русский язык,
автор: татьяна417
Предмет: Математика,
автор: катя5326
Предмет: Математика,
автор: dikow2006