Предмет: Геометрия,
автор: okostya523
Сторона основания правильной
шестиугольной пирамиды равна
4 см, а угол между боковой гранью
основанием равен 45°.
Найдите площадь боковой поверхности
пирамиды. В ответе укажите S/6.
Приложения:

Аноним:
4..
Ответы
Автор ответа:
2
Ответ:
24см
Объяснение:
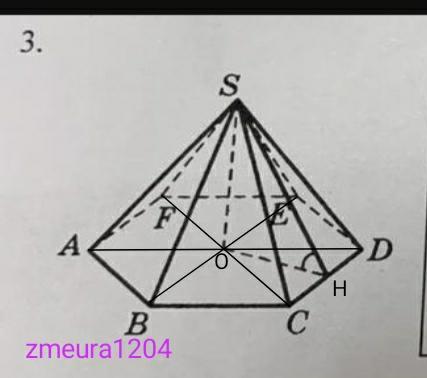
OH=CD*√3/2=4√3/2=2√3 см радиус вписанной окружности в шестиугольник.
∆SOH- равнобедренный треугольник (<SOH=90°, <OHS=45°; <OSH=45°) углы при основании равны.
SO=OH.
Теорема Пифагора
SH=√(SO²+OH²)=√((2√3)²+(2√3)²)=
=√√(12+12)=2√6 см.
Росн=6*АВ=6*4=24 см периметр шестиугольника.
Sбок=1/2*Росн*SH=1/2*24*2√6=24√6 см²
S/√6=24√6/√6=24см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: нат42
Предмет: Другие предметы,
автор: эля282
Предмет: Другие предметы,
автор: Dashidziya
Предмет: Математика,
автор: mayklplayx
Предмет: Математика,
автор: катя5326