Предмет: Геометрия,
автор: LelouchLamperouge1
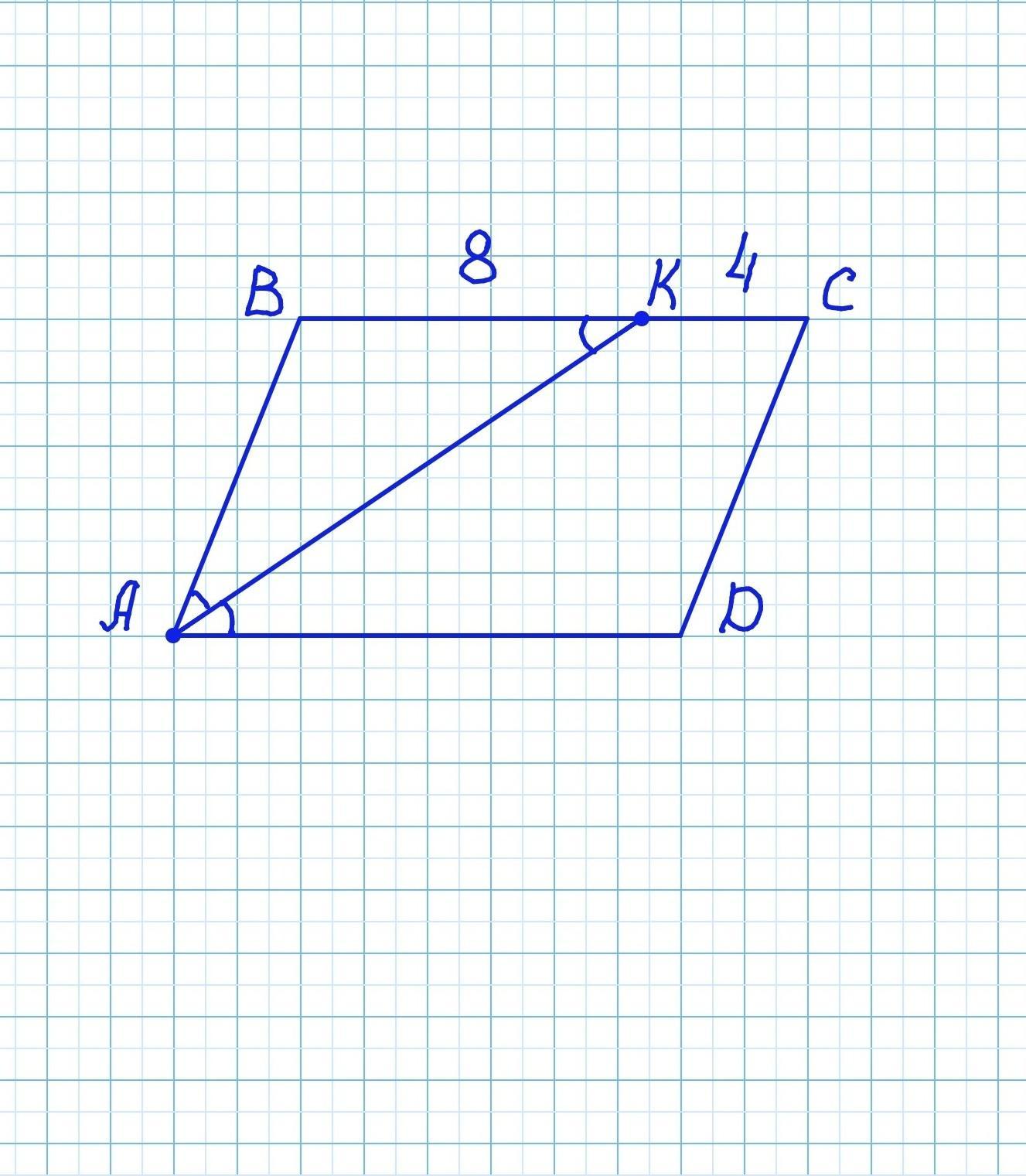
В параллелограмме ABCD угол A равен 50° и бисскетриса этого угла делит сторону BC на отрезки BK = 8 см и KC = 4 см. Найдите углы параллелограмма и его периметр
Ответы
Автор ответа:
4
Ответ:
∠А=∠С=50°,
∠В=∠D=130°,
BC=AD=12 см
АВ=CD=8см
Объяснение:
Свойства параллелограмма:
- Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180°
∠А+∠В=180°. ∠В=180°-∠А=180°-50°=130°.
- Противоположные углы параллелограмма равны.
∠D=∠B=130°; ∠C=∠A=50°.
- Противоположные стороны параллелограмма равны.
BC=BK+KC=8+4=12см. AD=BC=12см
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
Действительно, если AK - биссектриса угла А, то по свойству биссектрисы ∠BAК=∠KAD.
Но ∠KAD=∠ВKA, как внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущей АВ.
Следовательно ∠BAК=∠ВKA. А если углы при основании равны, то треугольник равнобедренный: △АВК - равнобедренный.
В равнобедренном треугольнике боковые стороны равны:
АВ=ВК=8см
DC=AB=8см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: agae
Предмет: Русский язык,
автор: asifgusejnov1
Предмет: Другие предметы,
автор: Ира1717
Предмет: Биология,
автор: astan4
Предмет: Другие предметы,
автор: vsempeaaaaas