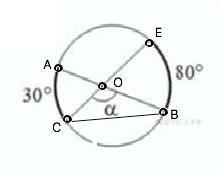
Решите задачу по данным рисунка

Ответы
На рисунке 3: Две хорды пересекаются внутри окружности. Найти градусную меру угла α, если величина противоположных дуг, отсекаемых хордами, 30° и 80°
Ответ: Угол α=125°
Объяснение:
Решить можно разными способами.
а) Обозначим хорды АВ и СЕ, точку их пересечения – О.
Угол между пересекающимися хордами равен полусумме дуг, заключённых между его сторонами и сторонами вертикального ему угла.
Следовательно, угол АОС=(◡АС+◡ВЕ):2=(30°+80°):2=55°
Смежный ему угол α=180°-55°=125°
* * *
б) Соединив т.С и т.В, получим треугольник СОВ. Его угол В - вписанный, опирается на дугу 30° и по свойству вписанного угла равен её половине. Угол ОВС=15°
Угол С - вписанный, опирается на дугу ВЕ и равен её половине. Угол ОСВ=40°.
Сумма углов треугольника 180°. =>
Угол α=180°-(15°+40°)=125°.
* * *
в) Градусная мера полной окружности 360°. Сумма двух известных дуг 30°+80°=110°.
Сумма двух других дуг 360°-110°=250°
Вертикальные углы, образуемые при пересечении хорд, равны. =>
Угол α=250°:2=125°