Предмет: Математика,
автор: anonimnyja142
Помогите пожалуйста. СРОЧНО. ОЧЕНЬ ПРОШУ.
1. Найти интеграл, используя метод разложения.
2. Найти интеграл, используя метод замены.
3.Найти интеграл, используя метод интегрирования по частям.
Приложения:
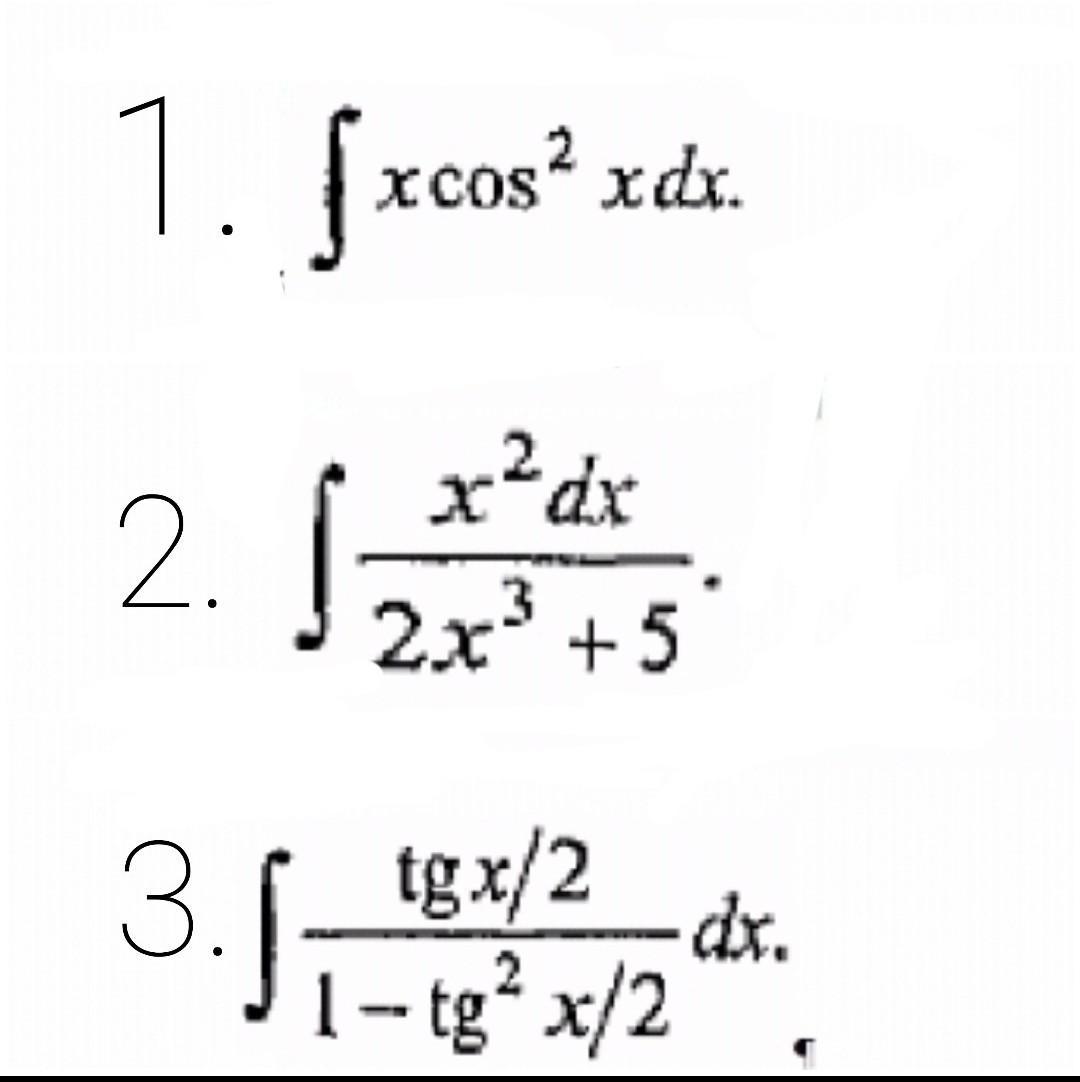
Ответы
Автор ответа:
2
Ответ:
1.
По частям:
2.
Замена:
3
Формула двойного угла:
anonimnyja142:
Огромное спасибо
Помоги пожалуйста, очень нужно. Прошу
Помоги пожалуйста, очень срочно
помогите пожалуйста, очень срочно
Похожие вопросы
Предмет: Русский язык,
автор: Алисочка1111
Предмет: Русский язык,
автор: pavlostrus
Предмет: Английский язык,
автор: nechaevaoli
Предмет: Химия,
автор: komissar1809
Предмет: Русский язык,
автор: Лидия123456