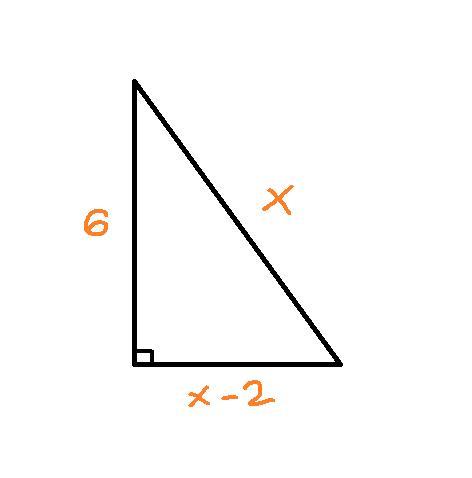Question

5. Один из катетов треугольника равно 6, а другой на 2 меньше гипотенузы.
Найдите площадь треугольника.​

Answer 1

Ответ:

AB=6 (катет 1)

AC=x (гиппотинуза)

BC=x-2 (катет 2)

Через Пифагора.

x^2=(x-2)^2+6^2

x^2=x^2-4x+4+36

4x=40

x=10 (AC)

BC=AC-2=8

S=AB*BC/2=6*8/2=24 см^2

Answer 2

Для нахождения площади прямоугольного треугольника используется следующая формула:

$S_{\triangle} = \frac{1}{2}ab,$

где $a$ и $b$ - катеты прямоугольного треугольника.

Нам известен один катет (6 см), значит, нужно найти другой. Поскольку катет на 2 меньше гипотенузы, то обозначим гипотенузу как $x$, а неизвестный катет как $x-2$ (см. изображение).

Для нахождения длины катета воспользуемся теоремой Пифагора:

$c^2 = a^2 + b^2$,

где $c$ - гипотенуза, а $a$ и $b$ - катеты.

Подставим известные значения:

$x^2 = 6^2 + (x-2)^2$

Раскроем скобки и выразим икс:

$x^2 = 36 + x^2 - 2x + 4\\x^2 = x^2 - 4x + 40\\4x = 40\\x = 10$

Мы нашли длину гипотенузы (т.к. обозначили её как $x$). Чтобы найти катет, просто вычтем из полученного значения 2:

$x-2 = 10-2 = 8$

Значит, катеты прямоугольного треугольника равны 6 и 8.

Теперь воспользуемся формулой нахождения площади (в самом начале):

$S_{\triangle} = \frac{1}{2}ab=\frac{1}{2}*6*8=\frac{48}{2} = 24$

Ответ: 24.