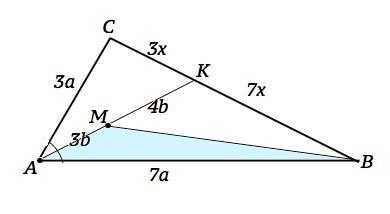
1. Площа трикутника ABC = 100 см². На бісектрисі АК позначили точку М так, що AM:MK=3:4.
Відомо, що АС:AB=3:7. Знайдіть площу трикутника ABM.
Будт ласка СРОЧНО
Ответы
Площадь треугольника ABC = 100 см². На биссектрисе АК обозначили точку М так, что AM: MK = 3: 4. Известно, что АС: AB = 3: 7. Найдите площадь треугольника ABM.
Ответ: 30 см²
Объяснение:
а) Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
⇒ СК:ВК=3:7; ∆ АСВ биссектрисой АК делится на два треугольника с общей высотой из вершины А и основаниями СК и ВК.
б) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
Примем коэффициент отношения оснований равным х. Тогда СВ=10х.
Ѕ ∆ АКВ=100:10•7=70 (см²)
В ∆ АКВ отношение площадей ∆ АМВ и ∆ КМВ равно отношению АМ:КМ. Примем коэффициент отношения оснований равным b. Тогда АК=7b, b=70:7=10 см², Ѕ(АВМ)=3•10=30 см²