Question

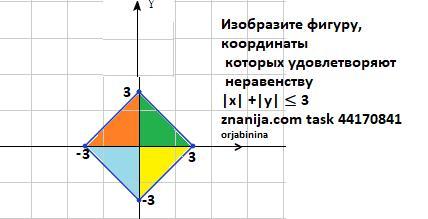
Изобразите фигуру, координаты которых удовлетворяют неравенству |x| +|y| ≤ 3​

Answer 1

Изобразите фигуру, координаты которых удовлетворяют неравенству

|x| +|y| ≤ 3​

Объяснение:   По определению модуля :

1) Пусть х>0 ,y>0,  тогда |x|=x, |y|=y. Получим х+у≤ 3 или у≤3-х , $\left \{ {{x>0} \atop {y>0}}\atop {y\leq 3-x} \right.$ .  Решением данной системы является часть плоскости ограниченная осями ох , оу и прямой у=3-х (на чертеже зеленая).

2) Пусть х>0 ,y≤0, тогда |x|=x, |y|=-y. Получим х-у≤ 3 или у≥х-3 , $\left \{ {{x>0} \atop {y\leq 0}}\atop {y\geq x-3} \right.$ .  Решением данной системы является часть плоскости ограниченная осями ох , оу и прямой у=х-3 ( на чертеже желтая) .

3) Пусть х≤0 ,y>0,  тогда |x|=-x, |y|=y. Получим -х+у≤ 3 или у≤3+х , $\left \{ {{x\leq 0} \atop {y>0}}\atop {y\leq 3+x} \right.$ .  Решением данной системы является часть плоскости ограниченная осями ох , оу и прямой у=3+х ( на чертеже красная ).

4) Пусть х≤0 ,y≤0, тогда |x|=-x, |y|=-y. Получим -х-у≤ 3 или у≥-х-3 , $\left \{ {{x\leq 0} \atop {y\leq 0}}\atop {y\geq -x-3} \right.$ .  Решением данной системы является часть плоскости ограниченная осями ох , оу и прямой у=-х-3( на чертеже голубая ).

        Тогда получается квадрат с внутренней частью и с вершинами в точках ( 0;3) , (3;0) , (0;-3) , (-3 ;0)  и "включенной границей"