Предмет: Алгебра,
автор: y9104231665
Помогите решить примеры
Приложения:
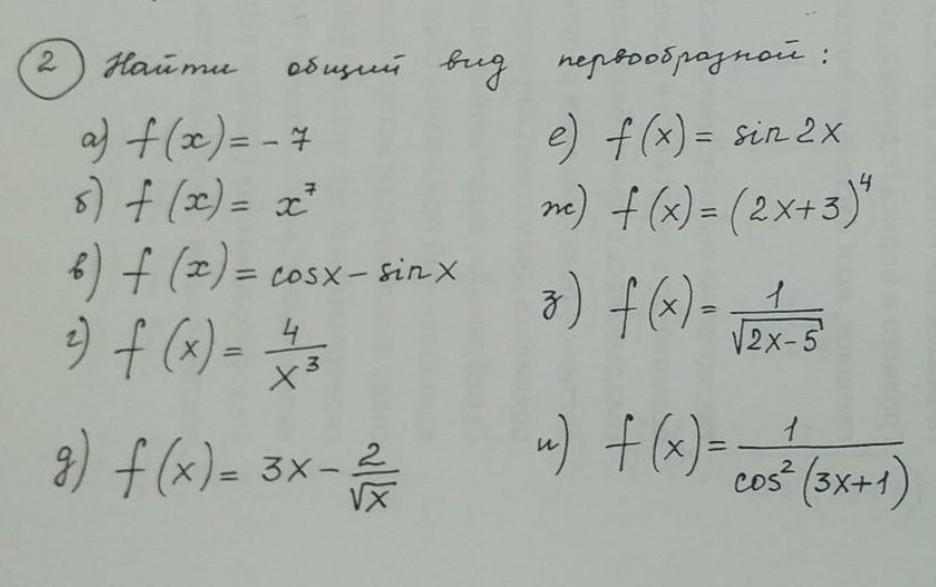
Ответы
Автор ответа:
0
Ответ:
а
б
в
г
д
е
ж
з
и
Похожие вопросы
Предмет: Русский язык,
автор: 777190
Предмет: Русский язык,
автор: школьник31к
Предмет: Русский язык,
автор: Коралина11111353
Предмет: Русский язык,
автор: Holamoss
Предмет: География,
автор: alenashakhbanova01