Question

отрезки АС и ВД диаметры окружности с центром О. Угол АСВ равен 19 градусам. найдите угол АОД. Ответ дайте в градусах​

Answer 1

Ответ:

∠AOD = 142°.

Объяснение:

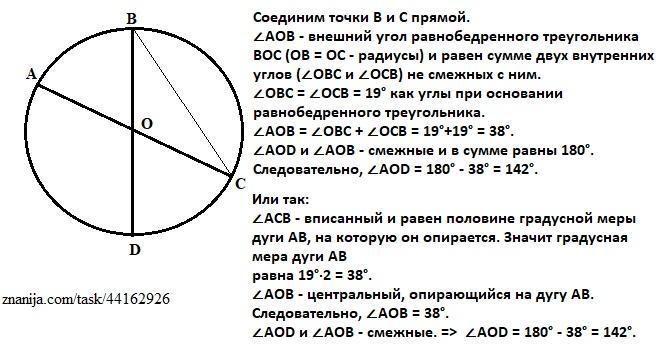
Отрезки АС и ВD -  диаметры окружности с центром О. ∠АСВ = 19°. найдите ∠АОD.  

Решение:

Соединим точки В и С прямой.

∠АОВ - внешний угол равнобедренного треугольника ВОС (ОВ = ОС - радиусы) и равен сумме двух внутренних углов (∠ОВС и ∠ОСВ) не смежных с ним. ∠ОВС = ∠ОСВ = 19° как углы при основании равнобедренного треугольника.

∠АОВ = ∠ОВС + ∠ОСВ = 19°+19° = 38°.

∠AOD и ∠АОВ - смежные и в сумме равны 180°.

Следовательно, ∠AOD = 180° - 38° = 142°.

Или так:

∠АСВ - вписанный и равен половине градусной меры дуги АВ, на которую он опирается. Значит градусная мера дуги АВ

равна 19°·2 = 38°.

∠АОВ - центральный, опирающийся на дугу АВ. Следовательно,

∠АОВ = 38°.

∠AOD и ∠АОВ - смежные. =>  ∠AOD = 180° - 38° = 142°.