Предмет: Алгебра,
автор: sudak1a
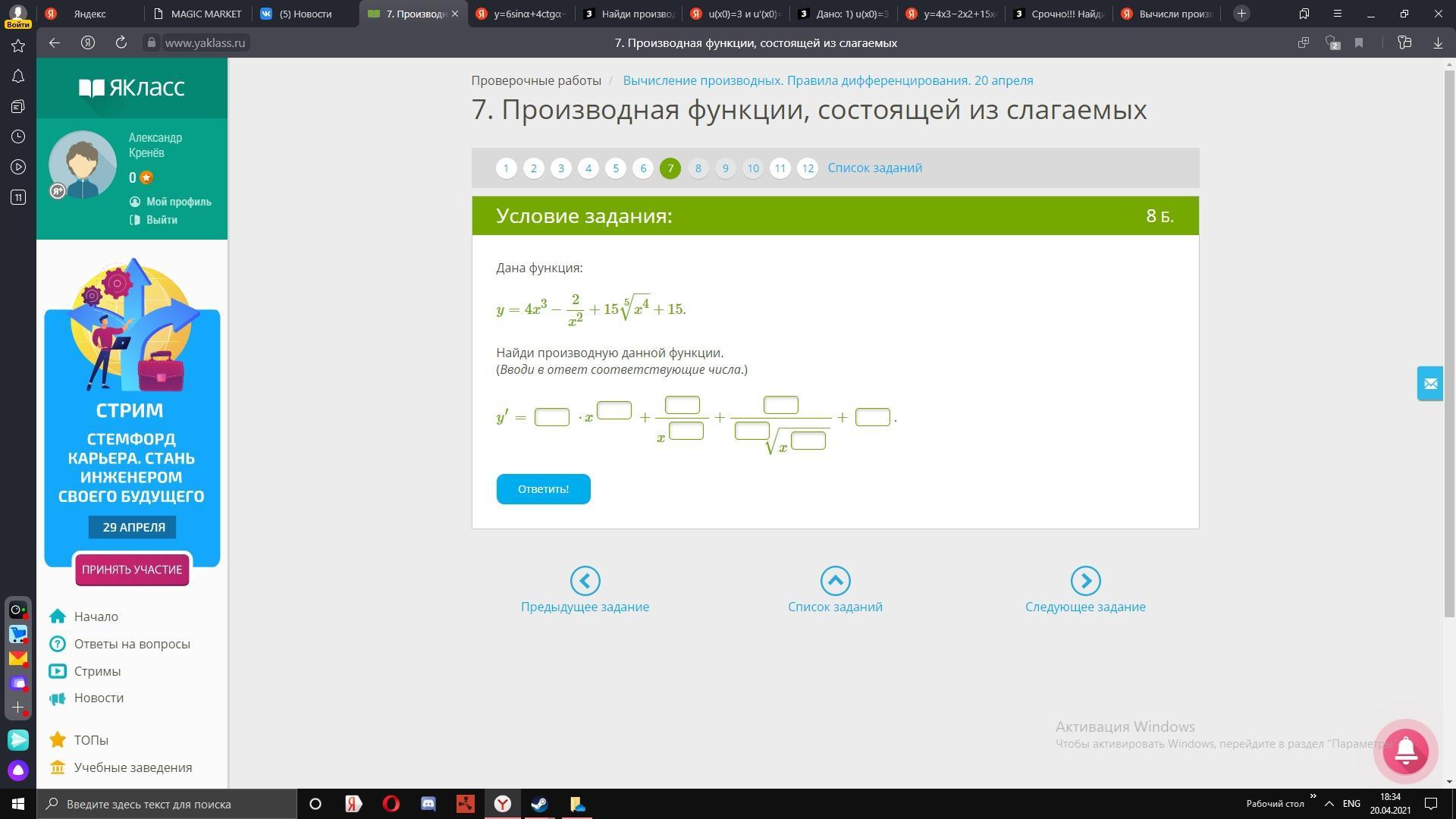
Помогите найти производную
Приложения:
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: feofilaktovale
Предмет: Русский язык,
автор: prokurorov
Предмет: Русский язык,
автор: Женька2005года
Предмет: Математика,
автор: Lubanyahaman
Предмет: Литература,
автор: boss2065