помогите сделать срочно!
Ответы
Ответ:
решения предоставленны на фото)
Пошаговое объяснение:
6 задача вот:
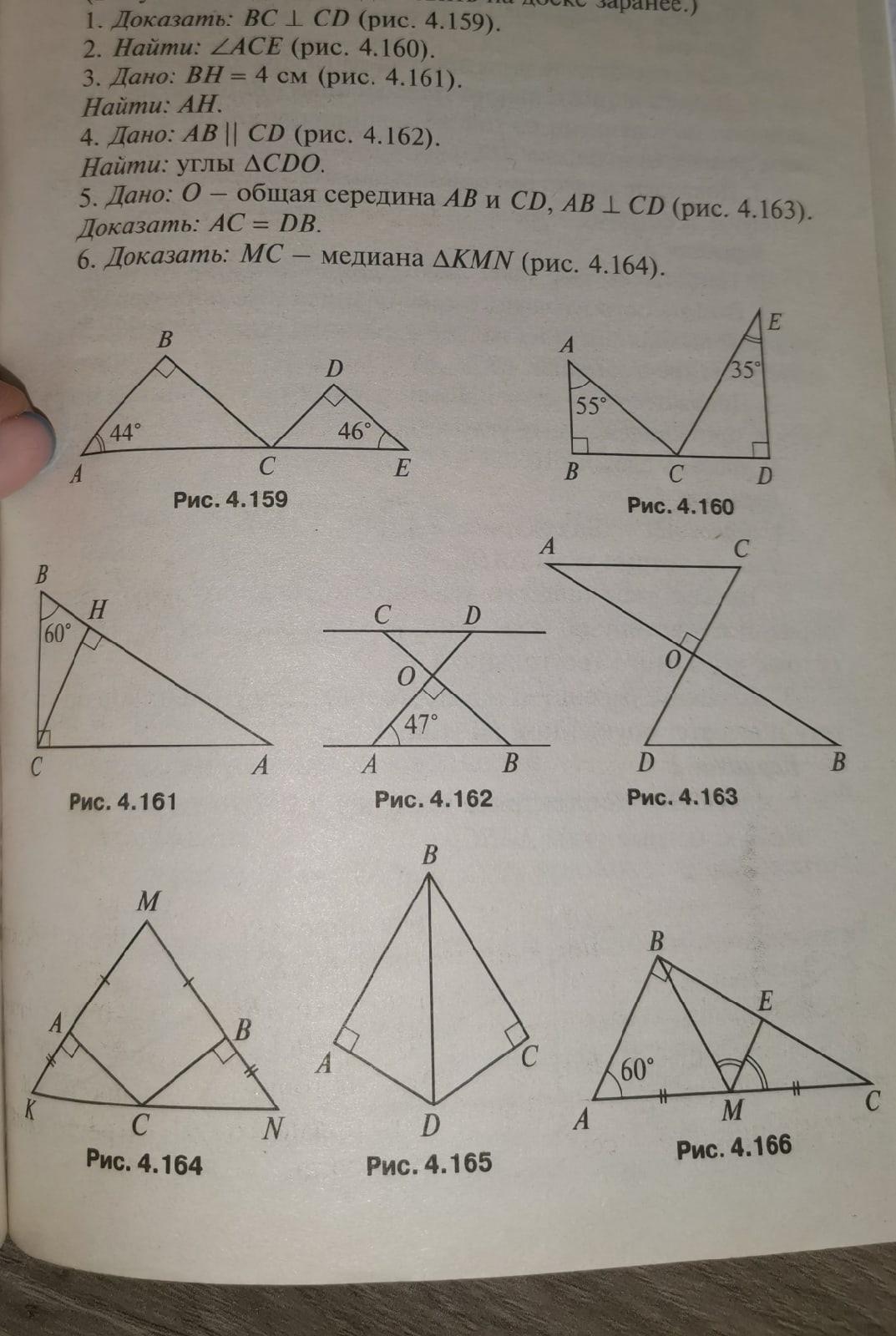
дано: треугольник КMN, AК-BN, AM-BM, СА перпендикулярно КМ, СВ перпендикулярно NM
доказать: МС -медиана треугольника КMN
В треугольнике КMN боковые стороны состоят из равных отрезков
АК-BN, AM-ВМ, следовательно
KM=MK+AM=BN+MB=MN
Треугольник КMN- равнобедренный.
△ КАС- △СВN,
так как это прямоугольные треугольники, углы К и N pавны как углы при основании равнобедренного треугольника,
катеты КА-BN.
Если в прямоугольном треугольнике острый угол и катет равен острому углу и катету другого прямоугольного треугольника, то эти треугольники равны.
Следовательно, гипотенузы АС и CN этих треугольников равны.
AC=CN
Точка С - середина стороны KN
MC - медиана треугольника КMN, что и требовалось доказать.




