Question

Знайди площу рівнобічної трапеції, одна з
основ, середня лінія та бічна сторона якої
відповідно дорівнюють 5 см, 8 см та 5 см.​

Answer 1

Ответ:

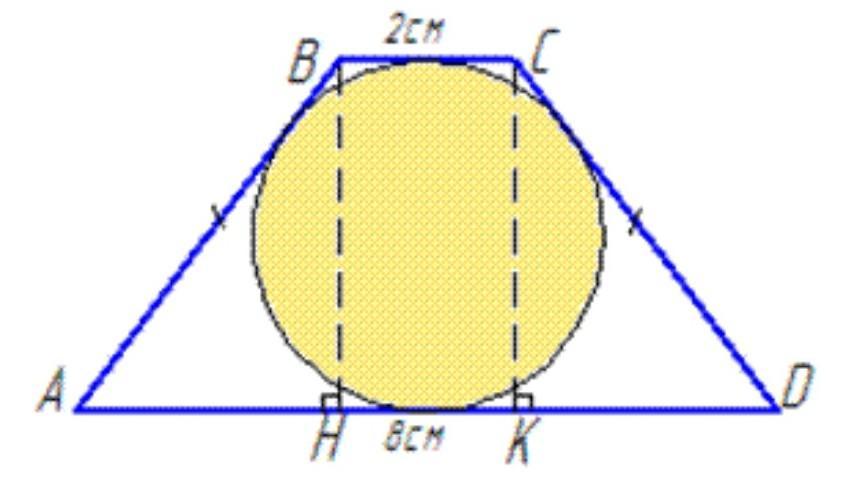
Нехай маємо рівнобічну трапецію ABCD, AD||BC, BC=2 см, AD=8 см, AB=CD, BH⊥AD, де BH– висота трапеції, опущена на сторону AD.

Оскільки у рівнобічну трапецію ABCD вписане коло, то суми її протилежних сторін рівні (за властивістю чотирикутника, описаного навколо кола), тобто AB+CD=AD+BC, звідси

2AB=8+2=10, AB=AD=10/2=5 см.

Опустимо ще одну висоту CK на сторону AD, тобто CK⊥AD (∠CKD=90).

Розглянемо прямокутні трикутники ABH і KCD.

У них ∠BAH=∠CKD – як кути при основі AD у рівнобічній трапеції ABCD (за властивістю), і CD=AB=5 см.

Тому, за ознакою рівності прямокутних трикутників, трикутники ABH і KCD рівні (за гіпотенузою і гострим кутом), і, отже, AH=KD=(8-2)/2=3 см.