Question

Геометрия
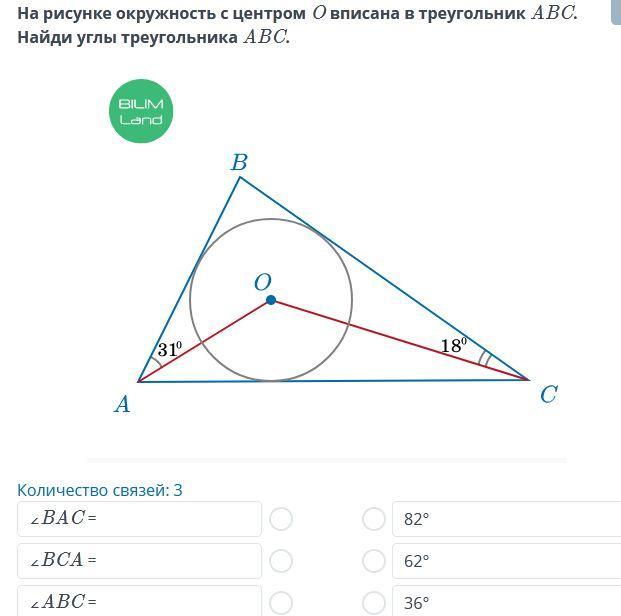
На рисунке окружность с центром O Вписана в треугольник ABC Найди углы треугольник ABC

Answer 1

Ответ:

Углы треугольник ABC: ∠ВАС=62°, ∠ВСА=36°, ∠АВС=82°

Объяснение:

В окружность с центром в точке О вписан треугольник АВС. Необходимо найти углы треугольника АВС.

Так как центром вписанной окружности является точка пересечения биссектрис треугольника, то АО является биссектрисой ∠ВАС.

• Биссектриса угла треугольника делит этот угол пополам.

Следовательно:∠ВАС=2•∠ВАО=2•31°=62°,

∠ВСА = 2•∠ВСО=2•18°=36°

• Сумма углов треугольника равна 180°

Значит ∠АВС=180°-∠ВАС-∠ВСА=180°-62°-36°=82°.

Ответ:∠ВАС=62°, ∠ВСА=36°, ∠АВС=82°